题目内容
12.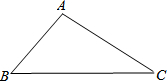 如图,已知在△ABC中,∠B=45°,AB=4cm,∠C=30°.求△ABC的面积(结果保留根号)
如图,已知在△ABC中,∠B=45°,AB=4cm,∠C=30°.求△ABC的面积(结果保留根号)
分析 过点A作AD⊥BC于D,得到两个直角三角形,根据锐角三角函数的定义,求出AD和BC的长,再计算出三角形的面积.
解答 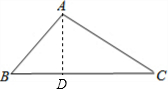 解:如图,过A作AD⊥BC于D,
解:如图,过A作AD⊥BC于D,
在Rt△ABD中,∵∠ADB=90°,∠B=45°,AB=4cm,
∴AD=AB•sinB=4×sin45°=2$\sqrt{2}$,
BD=AB•cosB=4×cos45°=2$\sqrt{2}$.
在Rt△ACD中,∵∠ADC=90°,∠C=30°,
∴CD=$\frac{AD}{tanC}$=$\frac{2\sqrt{2}}{tan30°}$=2$\sqrt{6}$,
∴BC=BD+CD=2$\sqrt{2}$+2$\sqrt{6}$,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×(2$\sqrt{2}$+2$\sqrt{6}$)×2$\sqrt{2}$=4+4$\sqrt{3}$(cm2).
点评 本题考查的是解直角三角形,过点A作BC的垂线段,把△ABC分成两个直角三角形,解这两个直角三角形,求出BC和AD的长,然后用三角形的面积公式求出三角形的面积.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
2.如果x2+2ax+b是一个完全平方公式,那么a与b满足的关系是( )
| A. | b=a | B. | a=2b | C. | b=2a | D. | b=a2 |
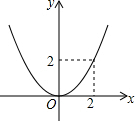 二次函数的图象如图所示.
二次函数的图象如图所示.