题目内容
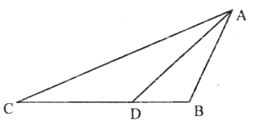
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一动点,
上一动点,![]() 于
于![]() ,
,![]() 于
于![]() .无论
.无论![]() 的位置如何变化,线段
的位置如何变化,线段![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
当AP⊥BC时,线段DE的值最小,利用四点共圆的判定可得A、E、P、D四点共圆且直径为AP得∠AED=∠C=45°,有一公共角,根据两角对应相等两三角形相似得△AED∽△ACB则![]() AD=2x,表示出AE和AC的长,求出AE与AC的比代入比例式中可求出DE的值
AD=2x,表示出AE和AC的长,求出AE与AC的比代入比例式中可求出DE的值
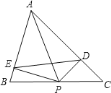
解:当AP⊥BC时线段DE的值最小
如图1,
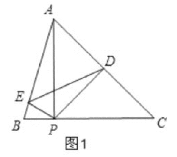
∵PE⊥AB,PD⊥AC,
∴∠AEP=∠ADP=90°,
∴∠AEP+∠ADP=180°,即A、E、P、D四点共圆且直径为AP
在Rt△PDC中,∠C=45°,
∴△PDC是等腰直角三角形,∠APD=45°,
∴△APD也是等腰直角三角形,∠PAD=45°,
∴∠PED=∠PAD=45°,
∴∠AED=45°,
∴∠AED=∠C=45°,
∵∠EAD=∠CAB,
∴△AED∽△ACB,
∴![]() ,
,
设AD=2x,则PD=DC=2x,AP=2![]() x,
x,
如图2
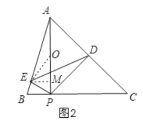
取AP的中点O连接EO则AO=OE=OP=![]() x
x
∵∠EAP=∠BAC-∠PAD=60°-45°=15°,
∴∠EOP=2∠EAO=30°
过E作EM⊥AP于M则EM=![]() x
x
cos30°=![]() ,
,
∴OM=![]() x·
x·![]() =
=![]() x,
x,
∴AM=![]() x,
x,
由勾股定理得:AE=![]() ,
,
∴![]() =
=![]() ,
,
∴ED=![]()
∴B选项是正确的

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
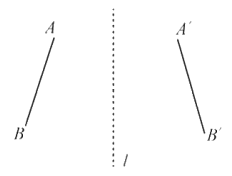
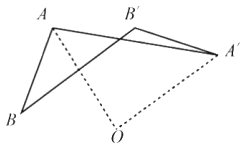
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
平移 |
| (1)__________. |
|
轴对称 |
| (2)__________. | (3)__________. |
旋转 |
|
| (4)__________. |