题目内容
方程x+| x |
| 1+2 |
| x |
| 1+2+3 |
| x |
| 1+2+3+…+2009 |
分析:本题将原方程变形,将大部分系数消掉,便可解答.
解答:解:原方程可化为:x(1+
+
+…+
)=2009;
即x(
+
+
+
+…+
)=2009;
提取公因式,得2x(1-
+
-
+
+
+…+
-
)=2009;
化简得:2x(1-
)=2009;
解得:x=1005.
| 1 |
| 1+2 |
| 1 |
| 1+2+3 |
| 1 |
| 1+2+3+…+2009 |
即x(
| 2 |
| 1×2 |
| 2 |
| 2×3 |
| 2 |
| 3×4 |
| 2 |
| 4×5 |
| 2 |
| 2009×2010 |
提取公因式,得2x(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2009 |
| 1 |
| 2010 |
化简得:2x(1-
| 1 |
| 2010 |
解得:x=1005.
点评:本题难度极大,需要很强的计算能力和创造性思维能力.要注意寻找规律(
=
,
=
-
).
| 1 |
| 1+2+3+…+n |
| 2 |
| n(n+1) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
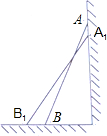 子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?