题目内容
1. 如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.
如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.(1)求$\widehat{BC}$的长.
(2)求弦BD的长.
分析 (1)首先根据AB是⊙O的直径,可得∠ACB=∠ADB=90°,然后在Rt△ABC中,求出∠BAC的度数,即可求出∠BOC的度数;最后根据弧长公式,求出$\widehat{BC}$的长即可.
(2)首先根据CD平分∠ACB,可得∠ACD=∠BCD;然后根据圆周角定理,可得∠AOD=∠BOD,所以AD=BD,∠ABD=∠BAD=45°;最后在Rt△ABD中,求出弦BD的长是多少即可.
解答 解:(1)如图,连接OC,OD,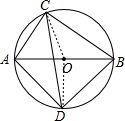 ,
,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
∵$cos∠BAC=\frac{AC}{AB}=\frac{5}{10}=\frac{1}{2}$,
∴∠BAC=60°,
∴∠BOC=2∠BAC=2×60°=120°,
∴$\widehat{BC}$的长=$\frac{120×π×(10÷2)}{180}=\frac{10}{3}π$.
(2)∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠AOD=∠BOD,
∴AD=BD,
∴∠ABD=∠BAD=45°,
在Rt△ABD中,
BD=AB×sin45°=10×$\frac{\sqrt{2}}{2}=5\sqrt{2}$.
点评 (1)此题主要考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,要熟练掌握.
(2)此题还考查了含30度角的直角三角形,以及等腰直角三角形的性质和应用,要熟练掌握.
(3)此题还考查了弧长的求法,要熟练掌握,解答此题的关键是要明确:①弧长公式:l=$\frac{nπR}{180}$(弧长为l,圆心角度数为n,圆的半径为R).②在弧长的计算公式中,n是表示1°的圆心角的倍数,n和180都不要带单位.

练习册系列答案
相关题目
12.下列命题是真命题的是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是正方形 |
9.数5的算术平方根为( )
| A. | $\sqrt{5}$ | B. | 25 | C. | ±25 | D. | ±$\sqrt{5}$ |
16.若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-2 |
6. 如图是一个可以自由转动的转盘,转盘分为6个大小相同的扇形,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),指针指向阴影区域的概率是( )
如图是一个可以自由转动的转盘,转盘分为6个大小相同的扇形,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),指针指向阴影区域的概率是( )
 如图是一个可以自由转动的转盘,转盘分为6个大小相同的扇形,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),指针指向阴影区域的概率是( )
如图是一个可以自由转动的转盘,转盘分为6个大小相同的扇形,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),指针指向阴影区域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
10.下列所述图形中,既是中心对称图形,又是轴对称图形的是( )
| A. | 矩形 | B. | 平行四边形 | C. | 正五边形 | D. | 正三角形 |

 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )