题目内容
已知AB=10cm,点C将AB分成两个部分,E,F分别是AC,BC的中点.
(1)AC=6cm,BC=4cm,求EF的长.
(2)若C为AB上任意一点,求EF的长.
 解:如图所示:
解:如图所示:(1)∵AC=6cm,BC=4cm,E,F分别是AC,BC的中点,
∴EC=
 AC=3cm,CF=
AC=3cm,CF= BC=2cm,
BC=2cm,∴EF=EC+CF=5cm;
(2)∵E,F分别是AC,BC的中点,
∴EC=
 AC,CF=
AC,CF= BC,
BC,∴EF=EC+CF=
 AC+
AC+ BC=
BC= (AC+BC)=
(AC+BC)= AB=5cm.
AB=5cm.分析:(1)先根据题意画出图形,再由线段中点的性质得出EC=3cm,CF=2cm,则EF=EC+CF=5cm;
(2)由线段中点的性质得出EC=
 AC,CF=
AC,CF= BC,则EF=EC+CF=
BC,则EF=EC+CF= AB=5cm.
AB=5cm.点评:本题考查的是两点间的距离,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
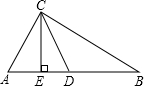 如图,在Rt△ABC中,CD是斜边上的中线,CE是高.已知AB=10cm,DE=2.5cm.
如图,在Rt△ABC中,CD是斜边上的中线,CE是高.已知AB=10cm,DE=2.5cm. 将直角△ABC沿斜边AB向右平移5cm,得到直角△DEF,已知AB=10cm,BC=8cm,AC=6cm,则右图中阴影部分三角形的面积为
将直角△ABC沿斜边AB向右平移5cm,得到直角△DEF,已知AB=10cm,BC=8cm,AC=6cm,则右图中阴影部分三角形的面积为 已知AB=10cm,点C在直线AB上,如果BC=4cm,点D是线段AC的中点,求线段BD的长度.
已知AB=10cm,点C在直线AB上,如果BC=4cm,点D是线段AC的中点,求线段BD的长度.