题目内容
如图，从山顶A望地面C、D两点，它们的俯角分别为30°、45°，若测得CD=100米，求AB的高度．（结果保留整数）
解：设AB=x，∵∠ADB=∠DAE=45°∴BD=AB=x
在Rt△ABC中，∠C=∠CAE=30°
∴tanC=
即
=
解得x=50
+50≈137
∴AB的高度为（50+50）米，即约为137米．
分析：首先根据题意分析图形；本题涉及到两个直角三角形，设AB=x，解这两个三角形可得BD与BC的大小，再利用CD=BC-BD=100，进而可求出答案．
点评：本题考查俯角的定义，要求学生能借助俯角构造直角三角形并结合图形利用三角函数解直角三角形．
在Rt△ABC中，∠C=∠CAE=30°
∴tanC=
即=解得x=50+50≈137∴AB的高度为（50
+50）米，即约为137米．分析：首先根据题意分析图形；本题涉及到两个直角三角形，设AB=x，解这两个三角形可得BD与BC的大小，再利用CD=BC-BD=100，进而可求出答案．
点评：本题考查俯角的定义，要求学生能借助俯角构造直角三角形并结合图形利用三角函数解直角三角形．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
如图，从山顶A望地面C、D两点，测得他们的俯角分别是45°和30°，已知CD=100米，点C位于BD上，求山AB的高度．（结果可保留根号）
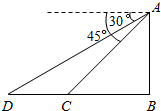如图，从山顶A望地面C、D两点，测得它们的俯角分别为45°和30°，已知CD=100米，点C在BD上，则山高AB=（ ）| A、100米 | ||
B、50
| ||
C、50
| ||
D、50(
|
如图，从山顶A望地面C、D两点，它们的俯角分别为30°、45°，若测得CD=100米，求AB的高度．（结果保留整数）
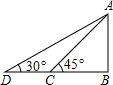如图，从山顶A望地面C，D两点，俯角分别为45°，30°，若CD=100米，则山高AB为（ ）| A、100米 | ||
B、50（
| ||
C、50
| ||
D、50
|
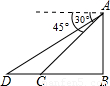
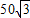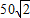米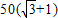
米
米