��Ŀ����
 ��۲����
��۲������a=5��b=3ʱ��
| a+b |
| 2 |
| ab |
��a=4��b=4ʱ��
| a+b |
| 2 |
| ab |
��̽��֤��
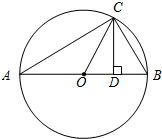
��ͼ��ʾ����ABCΪԲO���ڽ������Σ�ABΪֱ������C��CD��AB��D����AD=a��BD=b��
��1���ֱ���a��b��ʾ�߶�OC��CD��
��2��̽��OC��CD����ʽ֮����ڵĹ�ϵ���ú�a��b��ʽ�ӱ�ʾ����
����ɽ���
��������Ĺ۲���㡢̽��֤�������ܵó�
| a+b |
| 2 |
| ab |
��ʵ��Ӧ��
Ҫ�������Ϊ1ƽ���ij����ξ���ֱ������̽���ó��Ľ��ۣ���������ܳ�����Сֵ��
��������۲���㣺�ֱ������㼴�ɵó�
��
�Ĵ�С��ϵ��
��̽��֤����
��1������OC��ֱ��AB��һ�룬��OC�ã�ͨ��֤����ACD�ס�CBD������CD��
��2����a=b��a��b���ۿɵó�
��
�Ĵ�С��ϵ��
��ʵ��Ӧ�ã�ͨ��ǰ��Ľ��۳�����Ϊ������ʱ���ܳ���С��
| a+b |
| 2 |
| ab |
��̽��֤����
��1������OC��ֱ��AB��һ�룬��OC�ã�ͨ��֤����ACD�ס�CBD������CD��
��2����a=b��a��b���ۿɵó�
| a+b |
| 2 |
| ab |
��ʵ��Ӧ�ã�ͨ��ǰ��Ľ��۳�����Ϊ������ʱ���ܳ���С��
���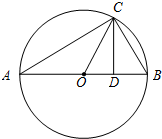 �⣺��۲���㣺
�⣺��۲���㣺
��
��
=
��
��̽��֤����
��1����AB=AD+BD=2OC��
��OC=
��ABΪ��Oֱ����
���ACB=90�㣮
�ߡ�A+��ACD=90�㣬��ACD+��BCD=90�㣬
���A=��BCD��
���ACD�ס�CBD��
��
=
��
��CD2=AD•BD=ab��
��CD=
��
��2����a=bʱ��OC=CD��
=
��
a��bʱ��OC��CD��
��
��
����۹��ɣ�
��
��
��ʵ��Ӧ��
�賤����һ�߳�Ϊx�ף�����һ�߳�Ϊ
�ף��辵���ܳ�Ϊl�ף���l=2(x+
)��4
=4��
��x=
����x=1���ף�ʱ�������ܳ���С��
��ʱ�ı���Ϊ������ʱ���ܳ���СΪ4�ף�
 �⣺��۲���㣺
�⣺��۲���㣺| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
��̽��֤����
��1����AB=AD+BD=2OC��
��OC=
| a+b |
| 2 |
��ABΪ��Oֱ����
���ACB=90�㣮
�ߡ�A+��ACD=90�㣬��ACD+��BCD=90�㣬
���A=��BCD��
���ACD�ס�CBD��
��
| AD |
| CD |
| CD |
| BD |
��CD2=AD•BD=ab��
��CD=
| ab |
��2����a=bʱ��OC=CD��
| a+b |
| 2 |
| ab |
a��bʱ��OC��CD��
| a+b |
| 2 |
| ab |
����۹��ɣ�
| a+b |
| 2 |
| ab |
��ʵ��Ӧ��
�賤����һ�߳�Ϊx�ף�����һ�߳�Ϊ
| 1 |
| x |
| 1 |
| x |
x•
|
��x=
| 1 |
| x |
��ʱ�ı���Ϊ������ʱ���ܳ���СΪ4�ף�
�����������ۺϿ����˼��β���ʽ�����������ε��ж������ʣ�ͨ�������֤���ó����ۣ�
��
�ǽ���Ĺؼ���
| a+b |
| 2 |
| ab |

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 �����⣮�۲����
�����⣮�۲���� ��
��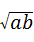 �Ĵ�С��ϵ��
�Ĵ�С��ϵ�� ��̽��֤��
��̽��֤�� ��
�� ��
�� �Ĵ�С��ϵ��
�Ĵ�С��ϵ�� ��̽��֤��
��̽��֤�� ��
�� ��
��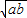 �Ĵ�С��ϵ��______
�Ĵ�С��ϵ��______