题目内容
7.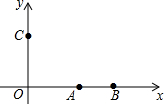 如图,已知点平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
如图,已知点平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )| A. | (6,8) | B. | (4,5) | C. | (4,$\frac{31}{8}$) | D. | (4,$\frac{33}{8}$) |
分析 根据题意可知点P的横坐标为4,设点P的坐标为(4,y),根据PA=PC列出关于y的方程,解方程得到答案.
解答  解:∵⊙P经过点A、B、C,
解:∵⊙P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),
作PE⊥OB于E,PF⊥OC与F,
由题意得,
$\sqrt{{4}^{2}+(y-4)^{2}}$=$\sqrt{{1}^{2}+{y}^{2}}$,
解得,y=$\frac{31}{8}$,
故选:C.
点评 本题考查的是确定圆的条件,解题的关键是理解经过不在同一直线上的三点作圆,圆心是过任意两点的线段的垂直平分线的交点.

练习册系列答案
相关题目
12.二次函数y=2x2的图象先向右平移1个单位,再向上平移3个单位后,所得到的抛物线的表达式为( )
| A. | y=2(x+1)2+3 | B. | y=2(x+1)2-3 | C. | y=2(x-1)2+3 | D. | y=2(x-1)2-3 |
17.下列四组线段中,可以构成直角三角形的是( )
| A. | 2,5,7 | B. | 4,5,6 | C. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | D. | 32,42,52 |
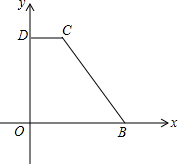 如图,在平面直角坐标系中,点B为x轴正半轴上一点,点D为y轴正半轴上一点,CD∥OB,OB=14,CD=2,BC=13.若两动点E、F同时从O点出发,其中点E以每秒1个单位的速度沿折线O→D→C移动,点F以每秒2个单位的速度从点O向点B移动.
如图,在平面直角坐标系中,点B为x轴正半轴上一点,点D为y轴正半轴上一点,CD∥OB,OB=14,CD=2,BC=13.若两动点E、F同时从O点出发,其中点E以每秒1个单位的速度沿折线O→D→C移动,点F以每秒2个单位的速度从点O向点B移动.