题目内容
18.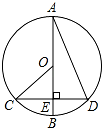 如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BOC=2∠BAD,则⊙O的直径为( )
如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BOC=2∠BAD,则⊙O的直径为( )| A. | 4 | B. | 5 | C. | 10 | D. | 3 |
分析 连结OD,先根据三角形外角性质得∠BOD=2∠A,而∠BOC=2∠BAD,所以∠BOC=∠BOD,根据等腰三角形的性质得OB⊥CD,则根据垂径定理得到CE=$\frac{1}{2}$CD=4,设⊙O的半径为R,则OE=AE-OA=8-R,在Rt△OCE中,根据勾股定理得R2=(8-R)2+42,解得R=5,故可得出结论.
解答 解:连结OD,如图,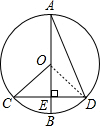
∵OA=OD,
∴∠A=∠ODA,
∴∠BOD=∠A+∠ODA=2∠A,
∵∠BOC=2∠BAD,
∴∠BOC=∠BOD,
而OC=OD,
∴OB⊥CD,
∴CE=DE=$\frac{1}{2}$CD=$\frac{1}{2}$×8=4,
设⊙O的半径为R,则OE=AE-OA=8-R,
在Rt△OCE中,
∵OC2=OE2+CE2,
∴R2=(8-R)2+42,解得R=5,即设⊙O的半径为5,
∴⊙O的直径为10.
故选C.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
9.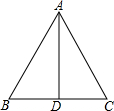 如图:△ABC中,D点在BC上,现有下列四个命题:①若AB=AC,则∠B=∠C.②若AB=AC,∠BAD=∠CAD,则AD⊥BC,BD=DC.③若AB=AC,BD=DC,则AD⊥BC,∠BAD=∠CAD.④若AB=AC,AD⊥BC,则BD=DC,∠BAD=∠CAD.其中正确的有( )
如图:△ABC中,D点在BC上,现有下列四个命题:①若AB=AC,则∠B=∠C.②若AB=AC,∠BAD=∠CAD,则AD⊥BC,BD=DC.③若AB=AC,BD=DC,则AD⊥BC,∠BAD=∠CAD.④若AB=AC,AD⊥BC,则BD=DC,∠BAD=∠CAD.其中正确的有( )
 如图:△ABC中,D点在BC上,现有下列四个命题:①若AB=AC,则∠B=∠C.②若AB=AC,∠BAD=∠CAD,则AD⊥BC,BD=DC.③若AB=AC,BD=DC,则AD⊥BC,∠BAD=∠CAD.④若AB=AC,AD⊥BC,则BD=DC,∠BAD=∠CAD.其中正确的有( )
如图:△ABC中,D点在BC上,现有下列四个命题:①若AB=AC,则∠B=∠C.②若AB=AC,∠BAD=∠CAD,则AD⊥BC,BD=DC.③若AB=AC,BD=DC,则AD⊥BC,∠BAD=∠CAD.④若AB=AC,AD⊥BC,则BD=DC,∠BAD=∠CAD.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.据统计:2014年,徐州市户籍人口约有950万人,用科学记数法表示这个数据为( )
| A. | 950×104 | B. | 95×105 | C. | 9.5×106 | D. | 0.95×107 |
3.下列式子错误的是( )
| A. | ±$\sqrt{0.04}$=±0.2 | B. | $\sqrt{0.09}$=±0.3 | C. | $\sqrt{(-5)^{2}}$=5 | D. | $\root{3}{-1000}$=-10 |
8.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a6 | C. | a6÷a2=a3 | D. | 23=6 |