题目内容
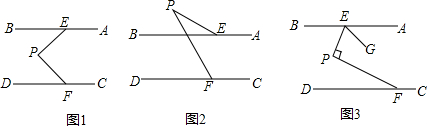
10.已知E,F分别是AB、CD上的动点,P也为一动点.(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD;
(2)如图2,若∠P=∠PFD-∠BEP,求证:AB∥CD;
(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求$\frac{∠AEG}{∠PFD}$的值.
分析 (1)过P作PQ平行于AB,由AB与CD平行,得到PQ与CD平行,利用两直线平行内错角相等得到两对角相等,再由∠EPF=∠1+∠2,等量代换就可得证;
(2)先根据三角形外角的性质得出∠P=∠BGP-∠BEP,再由∠P=∠PGB-∠BEP可知,∠PFD=∠PGB,由此可得出结论;
(3)由(1)中的结论∠EPF=∠BEP+∠PFD,设设∠PFD=x,则∠BEP=90°-x,根据∠PEG=∠BEP=90°-x,利用平角定义表示出∠AEG,即可求出所求比值.
解答 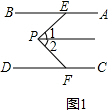 解:(1)过P作PQ∥AB,
解:(1)过P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD,
∴∠BEP=∠1,∠2=∠PFD,
∵∠EPF=∠1+∠2,
∴∠EPF=∠BEP+∠PFD;
(2)∵∠BGP是△PEG的外角,
∴∠P=∠BGP-∠BEP.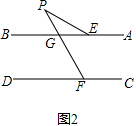
∵∠P=∠PGB-∠BEP,
∴∠PFD=∠PGB,
∴AB∥CD;
(3)由(1)的结论∠EPF=∠BEP+∠PFD=90°,
设∠PFD=x,则∠BEP=90°-x,
∵∠PEG=∠BEP=90°-x,
∴∠AEG=180°-2(90°-x)=2x,则$\frac{∠AEG}{∠PFD}$=$\frac{2x}{x}$=2
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理与性质、三角形外角的性质是解答此题的关键.

练习册系列答案
相关题目
20.下列判断正确的是( )
| A. | 有一条直角边对应相等的两个直角三角形全等 | |
| B. | 腰长相等的两个等腰三角形全等 | |
| C. | 斜边相等的两个等腰直角三角形全等 | |
| D. | 两个锐角对应相等的两个直角三角形全等 |
1.一列数:1,2,3,…,20.则这列数中是3的倍数的概率是( )
| A. | $\frac{3}{20}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{7}{20}$ |
5.直角坐标系中,P点在第四象限,则P点的坐标可能是( )
| A. | (6,-4) | B. | (5,2) | C. | (-3,-6) | D. | (-3,4) |
19.(2×102)3=( )
| A. | 2×106 | B. | 5×106 | C. | 8×106 | D. | 8×102 |
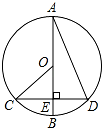 如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BOC=2∠BAD,则⊙O的直径为( )
如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BOC=2∠BAD,则⊙O的直径为( ) 如图,直线l:y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.
如图,直线l:y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.