Question

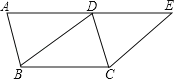
【题目】△ABC中，∠ACB=90°，AC=BC，D是BC上一点，连接AD，将线段AD绕着点A逆时针旋转，使点D的对应点E在BC的延长线上。过点E作EF⊥AD垂足为点G，

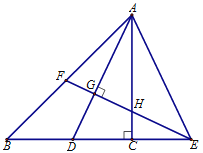
（1）求证：FE=AE；

（2）填空：=__________

（3）若，求的值(用含k的代数式表示)．

Answer 1

【答案】（1）证明见解析；（2）；（3）．

【解析】

（1）由，得，由∠AGH=∠ECH=90°，则∠DAC=∠BEF，由轴对称的性质，得到∠DAC=∠EAC，则∠BEF=∠EAC，利用三角形外角的性质，得到，即可得到结论成立；

（2）过点E作EM⊥BE，交BA延长线于点M，作AN⊥ME于N，先证明△BEF≌△MEA，

得到BF=AM，再利用等腰直角三角形的性质和矩形的性质，得到，DE=2CE=2AN，即可得到答案.

（3）根据题意，先证明，得到，从而得到，再证明，即可得到.

（1）证明：∵，

．

∵垂足为点，

．

∵,

．

∵，

．

∵,

．

在和中，，，，

．

．

∵,,

．

．

（2）如图，过点E作EM⊥BE，交BA延长线于点M，作AN⊥ME于N，

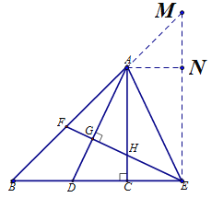
∵∠ACB=90°，AC=BC，

∴∠B=45°，

∵EM⊥BE，

∴∠M=∠B=45°，

∴BE=ME，

∵FE=AE，

∴△BEF≌△MEA，

∴BF=AM，

∵AN⊥ME，∠M=45°，

∴△AMN是等腰直角三角形，

∴AN=MN，AM=，

易知四边形ACEN是矩形，

∴CE=AN=MN，

∵DE=2CE=2AN，

∴;

故答案为：；

（3）解：如图：

∵，，

．

∵,

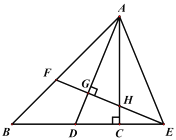
由（1）知，

．

由（1）知，

．

．

设，，则，，，．

．

．

∵，，

．

．