题目内容
20.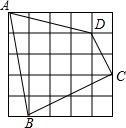 如图,网格中每个小正方形的边长都为1,
如图,网格中每个小正方形的边长都为1,(1)求四边形ABCD的面积;
(2)求∠BCD的度数.
分析 (1)利用正方形的面积减去四个顶点上三角形及小正方形的面积即可;
(2)连接BD,根据勾股定理的逆定理判断出△BCD的形状,进而可得出结论.
解答 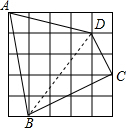 解:(1)S四边形ABCD=5×5-1-$\frac{1}{2}$×1×4-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×5=24-2-1-4-$\frac{5}{2}$=$\frac{29}{2}$;
解:(1)S四边形ABCD=5×5-1-$\frac{1}{2}$×1×4-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×5=24-2-1-4-$\frac{5}{2}$=$\frac{29}{2}$;
(2)连BD,
∵BC=2$\sqrt{5}$,CD=$\sqrt{5}$,BD=5,BC2+CD2=BD2,
∴∠BCD=90°.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
5.下列说法中正确的是( )
| A. | 已知a,b,c是三角形的三边长,则a2+b2=c2 | |
| B. | 在直角三角形中,两边长和的平方等于第三边长的平方 | |
| C. | 在Rt△ABC中,若∠C=90°,则三角形对应的三边满足a2+b2=c2 | |
| D. | 在Rt△ABC中,若∠A=90°,则三角形对应的三边满足a2+b2=c2 |
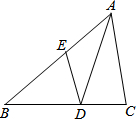 如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA.
如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA.
 小明和小刚用如图的两个转盘做配紫色的游戏,游戏规则是:分别旋转两个转盘,若其中的一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚得1分,否则小明得1分.此游戏规则公平吗?请说明理由.
小明和小刚用如图的两个转盘做配紫色的游戏,游戏规则是:分别旋转两个转盘,若其中的一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚得1分,否则小明得1分.此游戏规则公平吗?请说明理由.