题目内容
 如图,Rt△ABC的两条直角边BC=3,AC=4,斜边AB上的高为CD.若以C为圆心,分别以r1=2cm,r2=2.4cm,r3=3cm为半径作圆,试判断D点与这三个圆的位置关系.
如图,Rt△ABC的两条直角边BC=3,AC=4,斜边AB上的高为CD.若以C为圆心,分别以r1=2cm,r2=2.4cm,r3=3cm为半径作圆,试判断D点与这三个圆的位置关系.考点:点与圆的位置关系
专题:
分析:要判断点和圆的位置关系,需要比较圆心到直线的距离和圆的半径的大小.根据直角三角形的面积公式可以求得圆心到直线的距离,即直角三角形斜边上的高等于斜边的一半,则此题可解;
解答:解:作CD⊥AB于D.
在直角三角形ABC中,根据勾股定理得AB=5,则
CD=
=2.4;
①当r1=2cm,2.4>2,点D在圆外;
②当r2=2.4cm=d,点D在圆上;
③当r3=3cm时,2.4<3,点D在圆内.
在直角三角形ABC中,根据勾股定理得AB=5,则
CD=
| AC•BC |
| AB |
①当r1=2cm,2.4>2,点D在圆外;
②当r2=2.4cm=d,点D在圆上;
③当r3=3cm时,2.4<3,点D在圆内.
点评:本题考查了点与圆的位置关系,掌握直线和圆的位置关系与数量之间的联系:当d=r时,直线和圆相切;当d>r时,直线和圆相离;当d<r时,直线和圆相交.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知x-2y=-2,则3+2x-4y的值是( )
| A、0 | B、-1 | C、3 | D、5 |
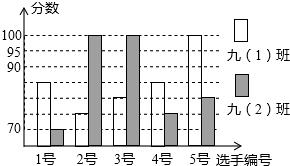 某中学开展“我的中国梦”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
某中学开展“我的中国梦”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示. 如图,在△ABC中,AB=AC,BC=20,△ABC的面积为
如图,在△ABC中,AB=AC,BC=20,△ABC的面积为 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,求∠C的度数和BE的长度.
如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,求∠C的度数和BE的长度.