题目内容
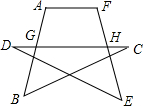如图，求∠A+∠B+∠C+∠D+∠E+∠F的度数．考点：多边形内角与外角,三角形内角和定理,三角形的外角性质
专题：
分析：由三角形外角性质得，∠AGH=∠B+∠C，∠FHG=∠D+∠E，从而求∠A+∠B+∠C+∠D+∠E+∠F的度数和，变为∠A+∠F+∠AGH+∠FHG的度数和，因∠A，∠F，∠AGH，∠FHG是四边形AGHF的四个内角，利用多边形的内角和定理：多边形的内角和=180°（n-2）即可求出它们的和．
解答：解：∵由三角形外角性质得，∠AGH=∠B+∠C，∠FHG=∠D+∠E，
∴∠A+∠B+∠C+∠D+∠E+∠F=∠A+∠F+∠AGH+∠FHG=180°×（4-2）=360°．
故∠A+∠B+∠C+∠D+∠E+∠F的度数是360°．
∴∠A+∠B+∠C+∠D+∠E+∠F=∠A+∠F+∠AGH+∠FHG=180°×（4-2）=360°．
故∠A+∠B+∠C+∠D+∠E+∠F的度数是360°．
点评：本题考查多边形的内角和定理，三角形的外角性质：三角形的一个外角等于和它不相邻的两个内角的和．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
菱形ABCD的边长为4，∠B=60°，F，H分别是AB，CD的中点，E，G分别在AD，BC上，且AE=CG
如图，△ABC与△AFG是两个全等的等腰直角三角形，∠BAC=∠F=90°，BC分别于AF、AG相交于点D、E，找出图中所有不全等的相似三角形并证明．若点A关于y轴的对称点是A（
，1），则点A的坐标为（ ）
| 1 |
| 2 |
A、（
| ||
B、（1，
| ||
C、（-
| ||
D、（
|