Question

如图，斜坡AB的坡比1：

3

，斜坡CD的坡比是1：1，AD=10+4

3

m，BC=6m，则从A经过斜坡到D的路程为

 

m．

Answer 1

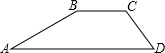
分析：分别过B、C作梯形的高BE，CF，则BE=CF，BC=EF，根据坡度的概念得到AE=

3

BE，CF=FD，设BE=x，得到

3

x+6+x=10+4

3

，解得x=4，则可得到AB=2x=8，CD=

2

x=2

2

，即可得到从A经过斜坡到D的路程．

解答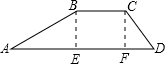：解：分别过B、C作梯形的高BE，CF，如图
∴BE=CF，BC=EF，
∵斜坡AB的坡比1：

3

，斜坡CD的坡比是1：1，
∴AE=

3

BE，CF=FD，
∴AB=2BE，CD=

2

CF，
设BE=x，则AE=

3

x，FD=x，
而AD=10+4

3

m，BC=6m，
∴

3

x+6+x=10+4

3

，解得x=4，
∴AB=2x=8，CD=

2

x=4

2

，
∴从A经过斜坡到D的路程=8+6+4

2

=（14+4

2

）m．
故答案为（14+4

2

）．

点评：本题考查了坡度的概念：斜坡的坡度等于斜坡的铅直高度与对应的水平距离的比值，即斜坡的坡度等于斜坡的坡角的正弦．也考查了特殊角的三角函数值．