题目内容
在等腰Rt△ABC中,AC=BC=2cm,D点为BC边中点,E为斜边AB上任意一点,则CE+DE的最小值为分析:首先确定动点E何位置时,DE+BE的值最小.即DC′=DE+EC′=DE+CE的值最小.然后根据勾股定理计算.
解答:解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于E,
此时DC′=DE+EC′=DE+CE的值最小.
连接CB′,易证CB′⊥BC,
根据勾股定理可得DC′=
cm.
此时DC′=DE+EC′=DE+CE的值最小.
连接CB′,易证CB′⊥BC,
根据勾股定理可得DC′=
| 5 |
点评:此题考查了线路最短的问题,确定动点E何位置时,使DE+BE的值最小是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 19、如图在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于D,若AB=10,则△BDE的周长等于
19、如图在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于D,若AB=10,则△BDE的周长等于 16、如图,在等腰Rt△ABC中,∠A=90°,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接OP将线段OP绕O逆时针旋转90°得到线段OD,要使点D恰好落在BC上,则AP的长度等于
16、如图,在等腰Rt△ABC中,∠A=90°,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接OP将线段OP绕O逆时针旋转90°得到线段OD,要使点D恰好落在BC上,则AP的长度等于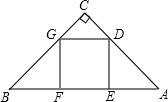 点G在边BC上.
点G在边BC上. (2013•怀化)如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(2013•怀化)如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.