题目内容
17、设a1,a2,…an,是n个任意给定的.求证:一定可以找到紧连在一起的若干个数,使得它们的和能被n整除.
分析:首先构造n个抽屉,被n除后余数可以为0、1、2、3、…(n-1),余数为0的符合题意,如果余数都不为0,则其中有两个余数相同,进一步作差问题得证.
解答:证明:根据题意构造抽屉{a1},{a1+a2},{a1+a2++an};
若其中某个被n整除,则问题得解;
否则它们被n除得的余数是1,2,,n-1共n-1个抽屉,
而{a1},{a1+a2},,{a1+a2++an}共n个数放入n-1个抽屉,
所以必有2个数在同一抽屉,则设其为a1+a2+…+ai与a1+a2+…+aj,
∴(a1+a2++ai)-(a1+a2++aj)=aj+1++ai能被n整除,
∴即可找到紧连在一起的若干个数,其和被n整除.
若其中某个被n整除,则问题得解;
否则它们被n除得的余数是1,2,,n-1共n-1个抽屉,
而{a1},{a1+a2},,{a1+a2++an}共n个数放入n-1个抽屉,
所以必有2个数在同一抽屉,则设其为a1+a2+…+ai与a1+a2+…+aj,
∴(a1+a2++ai)-(a1+a2++aj)=aj+1++ai能被n整除,
∴即可找到紧连在一起的若干个数,其和被n整除.
点评:此题关键是构造出抽屉,利用有余数的除法进行探讨数的整除性问题.

练习册系列答案
相关题目

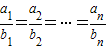 .
.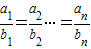 ,则
,则 .
.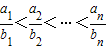 ,
,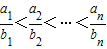 ,则 .
,则 .