题目内容
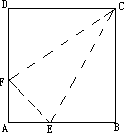
如图，小明将一张矩形纸片ABCD沿CE折叠，B点恰好落在AD边上，设此点为F，若AB：BC=3：5，求sin∠DCF的值是（ ）分析：由轴对称可以得知CF=CB，在Rt△DCF中由勾股定理表示出DF就可以求出结论．
解答：解：∵△EFC与△EBC关于CE成轴对称，
∴CF=CB．
∵AB：BC=3：5，设每份为x，
∴AB=3x，BC=5x．
∵四边形ABCD是矩形，
∴AD=BC，AB=CD，∠D=∠B=90°．
∴CD=3x，CF=5x．
在在Rt△DCF中由勾股定理，得
DF=4x．
∴sin∠DCF=
=
=
．
故选D．
∴CF=CB．
∵AB：BC=3：5，设每份为x，
∴AB=3x，BC=5x．
∵四边形ABCD是矩形，
∴AD=BC，AB=CD，∠D=∠B=90°．
∴CD=3x，CF=5x．
在在Rt△DCF中由勾股定理，得
DF=4x．
∴sin∠DCF=
| DF |
| CF |
| 4x |
| 5x |
| 4 |
| 5 |
故选D．
点评：本题考查了正方形的性质的运用，轴对称的性质的运用，勾股定理的运用，三角函数的运用，解答时运用勾股定理求出DF的值是关键．
练习册系列答案
相关题目
求sin∠DFC的值。