题目内容
20.已知⊙O的面积为4π,则其内接正方形的面积为( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
分析 作辅助线,根据圆的面积公式求出半径;根据勾股定理求出对角线长问题即可解决.
解答  解:如图,四边形ABCD为⊙O的内接正方形,连接AC、BD;
解:如图,四边形ABCD为⊙O的内接正方形,连接AC、BD;
设⊙O的半径为R,则πR2=4π,
∴R=2;
又∵∠ABC=90°,
∴AC为⊙O的直径,AC=2R=4;
∴其内接正方形的面积=$\frac{1}{2}$×4×4=8,
故选C.
点评 该题主要考查了圆内接正多边形的性质及其应用问题;解题的关键是灵活运用有关定理,熟练掌握正方形的面积求法.

练习册系列答案
相关题目
15.下列平面图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.若y=kx-4的函数值y随x的增大而减小,则k的值可能是下列的( )
| A. | -4 | B. | 0 | C. | 1 | D. | 3 |
9.已知P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数y=$\frac{2}{x}$的图象上的三点,且x1<x2<0<x3,则y1、y2、y3的大小关系是 ( )
| A. | y3<y2<y1 | B. | y2<y1<y3 | C. | y1<y2<y3 | D. | y2<y3<y1 |
10.|-2|的倒数是( )
| A. | 2 | B. | -$\frac{1}{2}$ | C. | -2 | D. | $\frac{1}{2}$ |
 如图,有两条公路OM,ON相交成30°角.沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
如图,有两条公路OM,ON相交成30°角.沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.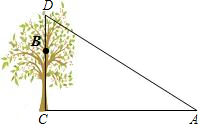 如图,一棵树CD,在其6m高的点B处有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树12m处的池塘A处,另一只猴子爬到树顶D后直线跃向池塘的A处.如果两只猴子所经过的路程相等,试问这棵树有多高?
如图,一棵树CD,在其6m高的点B处有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树12m处的池塘A处,另一只猴子爬到树顶D后直线跃向池塘的A处.如果两只猴子所经过的路程相等,试问这棵树有多高? 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①a>0;②b>0;③c<0;b2-4ac>0中,正确的个数有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①a>0;②b>0;③c<0;b2-4ac>0中,正确的个数有( )