题目内容
已知在Rt△ABC中,∠A,∠B,∠C对应的边分别为a,b,c,∠C=90°,c=34,且a:b=8:15,求Rt△ABC的周长.
考点:勾股定理
专题:
分析:根据题意设a=8x,b=15x,根据勾股定理可以求出x,进而求得a、b的值,即可求得Rt△ABC的周长.
解答:解:设a=8x,b=15x,
根据勾股定理:c2=a2+b2
即342=(8x)2+(15x)2,
解得x=2,
∴a=16,b=30,
∴C△ABC=a+b+c=78.
故Rt△ABC的周长为78.
根据勾股定理:c2=a2+b2
即342=(8x)2+(15x)2,
解得x=2,
∴a=16,b=30,
∴C△ABC=a+b+c=78.
故Rt△ABC的周长为78.
点评:本题考查的是勾股定理的灵活运用,题型比较简单,注意认真计算.

练习册系列答案
相关题目
 已知△ABC为等边三角形,直线a∥AB,D为直线BC上一点,∠ADE的一边DE交直线a于点E,∠ADE=60°,若D在BC上,求证:CD+CE=CA.
已知△ABC为等边三角形,直线a∥AB,D为直线BC上一点,∠ADE的一边DE交直线a于点E,∠ADE=60°,若D在BC上,求证:CD+CE=CA.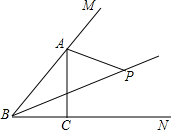 如图,点P为∠ABC和∠MAC的平分线的交点.求证:点P在∠ACN的平分线上.
如图,点P为∠ABC和∠MAC的平分线的交点.求证:点P在∠ACN的平分线上.