题目内容
如图，在△ABC中，∠B=75°，DE是AC的垂直平分线，且∠BAD：∠BAC=1：3，则∠C的度数是考点：线段垂直平分线的性质
专题：
分析：首先根据垂直平分线的性质可得AD=DC，然后再根据等边对等角可得∠C=∠DAC，再设∠BAD=x°，∠BAC=3x°，再利用三角形内角和可得方程，再解出x的值，进而可得∠C的度数．
解答：解：∵DE是AC的垂直平分线，
∴AD=DC，
∴∠C=∠DAC，
∵∠BAD：∠BAC=1：3，
∴设∠BAD=x°，∠BAC=3x°，
∴∠DAC=2x°，
∴∠C=2x°，
∵∠B=75°，
∴3x+2x+75=180，
解得：x=21，
∴∠C=42°．
故答案为：42．
∴AD=DC，
∴∠C=∠DAC，
∵∠BAD：∠BAC=1：3，
∴设∠BAD=x°，∠BAC=3x°，
∴∠DAC=2x°，
∴∠C=2x°，
∵∠B=75°，
∴3x+2x+75=180，
解得：x=21，
∴∠C=42°．
故答案为：42．
点评：此题主要考查了线段垂直平分线的性质，关键是掌握垂直平分线上任意一点，到线段两端点的距离相等．
练习册系列答案
计算高手系列答案
相关题目
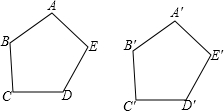如图，在五边形ABCDE和五边形A1B1C1D1E1中，如果AB=A1B1，BC=B1C1，CD=C1D1，DE=D1E1，EA=E1A1．请添加尽可能少的条件，使它们全等（写出添加的条件，不需要说明理由）
已知线段AB，请用尺规按下列要求作图（不写作法，只保留作图痕迹）：
