题目内容
15.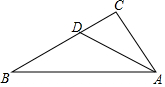 如图所示,△ABC中,∠C=90°,AD平分∠BAC,AB=7cm,CD=3cm,则△ABD的面积是$\frac{21}{2}$cm2.
如图所示,△ABC中,∠C=90°,AD平分∠BAC,AB=7cm,CD=3cm,则△ABD的面积是$\frac{21}{2}$cm2.
分析 过点D作DE⊥AB,由角平分线的性质可知DE=CD=3,再根据S△ABD=$\frac{1}{2}$AB•DE即可得出结论.
解答  解:过点D作DE⊥AB,
解:过点D作DE⊥AB,
∵AD平分∠BAC,
∴DE=CD=3,
S△ABD=$\frac{1}{2}$AB×DE=$\frac{1}{2}$×7×3=$\frac{21}{2}$cm2.
故答案为:$\frac{21}{2}$cm2.
点评 本题考查的是角平分线的性质及三角形的面积公式,根据题意作出辅助线是解答此题的关键.

练习册系列答案
相关题目
6.在射击训练中,小强哥哥射击了五次,成绩(单位:环)分别为:8,9,7,10,9,这五次成绩的众数和中位数分别是( )
| A. | 9,9 | B. | 7,9 | C. | 9,7 | D. | 8,9 |
7.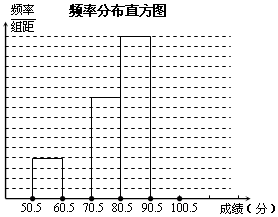 为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
频数分布表
(1)频数分布表中a=12;b=50;
(2)补全频数分布直方图;(3)在该问题中的样本容量是50;
(4)全体参赛学生中,竞赛成绩落在80.5~90.5组范围内的人数最多;
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为216人.
 为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:频数分布表
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 008 |
| 60.5~70.5 | 8 | b |
| 70.5~80.5 | 10 | 020 |
| 80.5~90.5 | 16 | 032 |
| 90.5~100.5 | a | 0.24 |
| 合计 |
(2)补全频数分布直方图;(3)在该问题中的样本容量是50;
(4)全体参赛学生中,竞赛成绩落在80.5~90.5组范围内的人数最多;
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为216人.
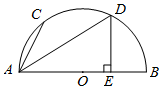 如图,C、D两点在以AB为直径的半圆O上,AD平分∠BAC,AB=20,AD=4$\sqrt{15}$,DE⊥AB于E.
如图,C、D两点在以AB为直径的半圆O上,AD平分∠BAC,AB=20,AD=4$\sqrt{15}$,DE⊥AB于E.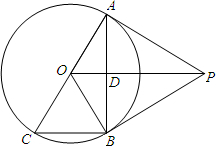 如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,AB是弦,PA∥BC交AB于点D
如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,AB是弦,PA∥BC交AB于点D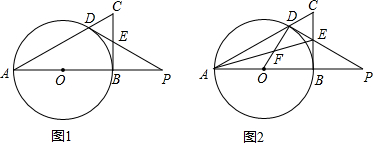
 如图,在平行四边形ABCD中,BC=6cm,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形.求:
如图,在平行四边形ABCD中,BC=6cm,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形.求: