题目内容
6.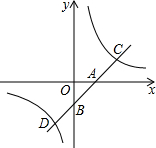 如图所示,直线y=kx+b分别交x轴、y轴于点A(1,0),B(0,-1),交双曲线y=$\frac{m}{x}$于点C,D,且AB=AC.
如图所示,直线y=kx+b分别交x轴、y轴于点A(1,0),B(0,-1),交双曲线y=$\frac{m}{x}$于点C,D,且AB=AC.(1)求直线及双曲线的函数解析式;
(2)直接写出不等式kx+b>$\frac{m}{x}$的解集.
分析 (1)如图,作CH⊥x轴于H.设直线AB的解析式为y=kx+b,利用待定系数法求出k、b,利用△AOB∽△AHC,推出AH=OA=1,CH=OB=1,推出C(2,1),利用待定系数法即可求出m.
(2)根据一次函数的图象在反比例函数的图象上方,确定变量x的取值范围即可.
解答 解:(1)如图,作CH⊥x轴于H.设直线AB的解析式为y=kx+b,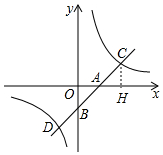
把(A(1,0),B(0,-1)代入得$\left\{\begin{array}{l}{b=-1}\\{k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
∴直线AB的解析式为y=x-1.
在△AOB和△AHC中,
$\left\{\begin{array}{l}{∠OAB=∠CAH}\\{∠AOB=∠AHC}\\{AB=AC}\end{array}\right.$,
∴△AOB∽△AHC,
∴AH=OA=1,CH=OB=1,
∴C(2,1),
把C(2,1)代入y=$\frac{m}{x}$中,得到m=2,
∴反比例函数的解析式为y=$\frac{2}{x}$.
(2)由$\left\{\begin{array}{l}{y=x-1}\\{y=\frac{2}{x}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,
∵C(2,1),
∴D(-1,-2),
由图象可知,不等式kx+b>$\frac{m}{x}$的解集为-1<x<0或x>2.
点评 本题考查一次函数与反比例函数的交点问题、待定系数法等知识,解题的关键是灵活运用待定系数法确定函数解析式,学会利用方程组求两个函数图象的交点坐标,学会根据图象,确定自变量的取值范围,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案 如图,在平面直角坐标系中,小猫遮住的点的坐标可能是( )
如图,在平面直角坐标系中,小猫遮住的点的坐标可能是( )| A. | (-2,1) | B. | (2,3) | C. | (3,-5) | D. | (-6,-2) |
| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
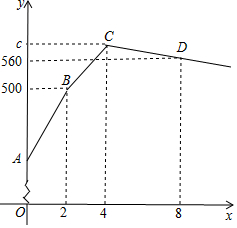 某手工编织厂生产一种旅游纪念品,现有60名工人进行手工编织(每人编织的效率相同),2天后抽出10名工人执行其他任务,其余工人继续编织生产;2天后从编织的工人中再抽出10名进行销售(每人每天的销售量相同).已知每人每天的销售量是编织量的5倍,下图是产品库存量y(件)与生产时间x(天)之间的函数关系图象.
某手工编织厂生产一种旅游纪念品,现有60名工人进行手工编织(每人编织的效率相同),2天后抽出10名工人执行其他任务,其余工人继续编织生产;2天后从编织的工人中再抽出10名进行销售(每人每天的销售量相同).已知每人每天的销售量是编织量的5倍,下图是产品库存量y(件)与生产时间x(天)之间的函数关系图象.