题目内容
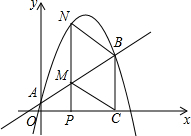 如图,直线y=
如图,直线y=| 1 |
| 2 |
| 17 |
| 4 |
(1)求抛物线的解析式.
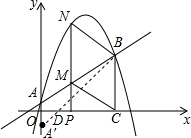
(2)在x轴上是否存在一点D,使AD+BD最短?若存在,请求出点D坐标;若不存在,请说明理由.
(3)点P(t,0)为线段OC上任一点(不与点O、C重合),过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.
①求MN的最大值;
②连接CM、BN,试求:当t为何值时,四边形BCMN为菱形?
考点:二次函数综合题
专题:压轴题
分析:(1)先令x=0求出y的值即可得出A点坐标,再把C点横坐标代入直线y=
x+1求出y的值即可得出B点坐标,把AB两点坐标代入抛物线即可得出a、c的值,故可得出抛物线的解析式;
(2)作出点A关于x轴的对称点A′,连接A′B,则线段A′B的长即为AD+BD最短,再利用待定系数法求出直线A′B的解析式,故可得出D点坐标;
(3)①先用含t的代数式表示P、M、N的坐标,再根据MN=NP-MP,即可得到线段MN的长与t的函数关系式为MN,然后运用配方法可求出MN的最大值;
②若四边形BCMN为平行四边形,则有MN=BC,故可得出关于t的二元一次方程,解方程求得t的值,再分别分析t取何值时四边形BCMN为菱形即可.
| 1 |
| 2 |
(2)作出点A关于x轴的对称点A′,连接A′B,则线段A′B的长即为AD+BD最短,再利用待定系数法求出直线A′B的解析式,故可得出D点坐标;
(3)①先用含t的代数式表示P、M、N的坐标,再根据MN=NP-MP,即可得到线段MN的长与t的函数关系式为MN,然后运用配方法可求出MN的最大值;
②若四边形BCMN为平行四边形,则有MN=BC,故可得出关于t的二元一次方程,解方程求得t的值,再分别分析t取何值时四边形BCMN为菱形即可.
解答:解:(1)∵令x=0,则y=1,
∴A(0,1),
∵BC⊥x轴,C(3,0),
∴当x=3时,y=
×3+1=
,
∴B(3,
),
∵AB两点均在抛物线y=ax2+
x+c上,
∴
,解得
,
∴抛物线的解析式为:y=-
x2+
x+1;
(2)作出点A关于x轴的对称点A′,连接A′B,则线段A′B的长即为AD+BD最短,
∵A(0,1),B(3,
),
∴A′(0,-1),
设直线A′B的解析式为y=kx+b(k≠0),
∴
,解得
,
∴直线A′B的解析式y=
x-1;
∴当y=0时,
x-1=0,解得x=
,
∴D(
,0);
(3)①∵P(t,0),
∴M(t,
t+1),N(t,-
t2+
t+1),
∴MN=NP-MP=(-
t2+
t+1)-(
t+1)=-
t2+
t,即线段MN的长与t的函数关系式为MN=-
t2+
t(0≤t≤3);
∵-
t2+
t=
(t2-3t)=-
(t-
)2+
,
∴当t=
时,MN的长最大,最大值是
;
②∵若四边形BCMN为平行四边形,
∴MN=BC,即-
t2+
t=
,解得t1=1,t2=2,
∴当t=1或2时,四边形BCMN为平行四边形;
当t=1时,MN=-
×12+
×1=
,MP=
×1+1=
,PC=3-1=2,
在Rt△MPC中,MC=
=
=
,
∴MN=MC,此时平行四边形BCMN为菱形;
当t=2时,MN=-
×22+
×2=
,MP=
×2+1=2,PC=3-2=1,
在Rt△MPC中,MC=
=
=
∴MN≠MC,此时平行四边形BCMN不是菱形.
∴当t=1时,四边形BCMN为菱形.
∴A(0,1),
∵BC⊥x轴,C(3,0),
∴当x=3时,y=
| 1 |
| 2 |
| 5 |
| 2 |

∴B(3,
| 5 |
| 2 |
∵AB两点均在抛物线y=ax2+
| 17 |
| 4 |
∴
|
|
∴抛物线的解析式为:y=-
| 5 |
| 4 |
| 17 |
| 4 |
(2)作出点A关于x轴的对称点A′,连接A′B,则线段A′B的长即为AD+BD最短,
∵A(0,1),B(3,
| 5 |
| 2 |
∴A′(0,-1),
设直线A′B的解析式为y=kx+b(k≠0),
∴
|
|
∴直线A′B的解析式y=
| 7 |
| 6 |
∴当y=0时,
| 7 |
| 6 |
| 6 |
| 7 |
∴D(
| 6 |
| 7 |
(3)①∵P(t,0),
∴M(t,
| 1 |
| 2 |
| 5 |
| 4 |
| 17 |
| 4 |
∴MN=NP-MP=(-
| 5 |
| 4 |
| 17 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
| 5 |
| 4 |
| 15 |
| 4 |
∵-
| 5 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
| 5 |
| 4 |
| 3 |
| 2 |
| 45 |
| 16 |
∴当t=
| 3 |
| 2 |
| 45 |
| 16 |
②∵若四边形BCMN为平行四边形,
∴MN=BC,即-
| 5 |
| 4 |
| 15 |
| 4 |
| 5 |
| 2 |
∴当t=1或2时,四边形BCMN为平行四边形;
当t=1时,MN=-
| 5 |
| 4 |
| 15 |
| 4 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
在Rt△MPC中,MC=
| MP2+PC2 |
(
|
| 5 |
| 2 |
∴MN=MC,此时平行四边形BCMN为菱形;
当t=2时,MN=-
| 5 |
| 4 |
| 15 |
| 4 |
| 5 |
| 2 |
| 1 |
| 2 |
在Rt△MPC中,MC=
| MP2+PC2 |
| 22+12 |
| 5 |
∴MN≠MC,此时平行四边形BCMN不是菱形.
∴当t=1时,四边形BCMN为菱形.
点评:本题考查了的是二次函数综合题,涉及到待定系数法求二次函数的解析式,线段的长与函数关系式之间的关系,二次函数的性质,平行四边形以及菱形的性质与判定,勾股定理等知识,综合性较强,难度较大,解题的关键是数形结合思想与方程思想的应用.

练习册系列答案
相关题目
实数3、3.14、
、
、
、-
中,有理数的个数为( )
| 2 |
| 3 | -27 |
| 13 |
| 8 |
| π |
| 3 |
| A、2 | B、3 | C、4 | D、5 |
 如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=
如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=| 2 |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
直角三角形的三边长是连续偶数,则三边长分别是( )
| A、2,4,6 |
| B、4,6,8 |
| C、6,8,10 |
| D、8,10,12 |
 2013年4月20日早晨8时02分,四川省雅安市芦山县发生7.0级地震,举国上下纷纷捐款捐物.某陶艺班学生积极参与赈灾,决定制作A、B两种型号陶艺品进行义卖,将所得善款全部捐给灾区,制作这两类陶艺品时需用甲、乙两种材料,制作A、B两种型号陶艺品的用料情况如下表所示:
2013年4月20日早晨8时02分,四川省雅安市芦山县发生7.0级地震,举国上下纷纷捐款捐物.某陶艺班学生积极参与赈灾,决定制作A、B两种型号陶艺品进行义卖,将所得善款全部捐给灾区,制作这两类陶艺品时需用甲、乙两种材料,制作A、B两种型号陶艺品的用料情况如下表所示: 如图,已知平行四边形ABCD中,E、F分别为AB、CD上的点,且AE=
如图,已知平行四边形ABCD中,E、F分别为AB、CD上的点,且AE= 如图,AB=AC,D,E分别是AB,AC的中点,请说明△BOC是等腰三角形的理由.
如图,AB=AC,D,E分别是AB,AC的中点,请说明△BOC是等腰三角形的理由. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2