题目内容
 如图,已知平行四边形ABCD中,E、F分别为AB、CD上的点,且AE=
如图,已知平行四边形ABCD中,E、F分别为AB、CD上的点,且AE=| 1 |
| 4 |
| 1 |
| 4 |
考点:平行四边形的判定与性质
专题:证明题
分析:连接DE、BF.根据DF=EB,且DF∥BE证明四边形DEBF是平行四边形.再根据平行四边形的性质:对角线互相平分得到EF与BD互相平分.
解答: 证明:如图,∵四边形ABCD是平行四边形,
证明:如图,∵四边形ABCD是平行四边形,
∴AB∥DC即EB∥DF,且AB=DC.
又∵AE=
AB,CF=
CD,
∴AE=CF,
∴AB=AE=DC-CF,即EB=DF,
∴边形DEBF是平行四边形,
∴BD与EF互相平分.
 证明:如图,∵四边形ABCD是平行四边形,
证明:如图,∵四边形ABCD是平行四边形,∴AB∥DC即EB∥DF,且AB=DC.
又∵AE=
| 1 |
| 4 |
| 1 |
| 4 |
∴AE=CF,
∴AB=AE=DC-CF,即EB=DF,
∴边形DEBF是平行四边形,
∴BD与EF互相平分.
点评:本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 如图,在△ABC与△CBE中,已知BD=BE,∠ABD=∠CBE,在添加下列一个条件后,不能说明△ABC与△CBE全等的是( )
如图,在△ABC与△CBE中,已知BD=BE,∠ABD=∠CBE,在添加下列一个条件后,不能说明△ABC与△CBE全等的是( )| A、AB=CB |
| B、AD=CE |
| C、∠A=∠C |
| D、∠D=∠E |
 如图,抛物线y=ax2+bx+2与x轴交于A、B两点,点A的坐标为(-1,0),抛物线的对称轴为直线
如图,抛物线y=ax2+bx+2与x轴交于A、B两点,点A的坐标为(-1,0),抛物线的对称轴为直线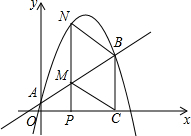 如图,直线y=
如图,直线y= 如图,CD平分∠ACB交AB于点D,DE∥BC交AC于点E,DF∥AC交BC于点F,那么四边形DFCE是
如图,CD平分∠ACB交AB于点D,DE∥BC交AC于点E,DF∥AC交BC于点F,那么四边形DFCE是 如图,已知AB=AD,BC=CD,请说明
如图,已知AB=AD,BC=CD,请说明