Question

在菱形ABCD中，∠BAD=θ，△AEF为正三角形，E、F在菱形边上．请你操作，探索：当θ分别满足下列条件时，能否作出菱形的内接正三角形AEF（E、F分别在菱形边上）？请填写下表．（表下方的菱形供探索用）

满足的条件	0°＜θ＜60°	θ=60°	60°＜θ＜120°	θ=120°	120°＜θ＜180°
内接正△AEF个数	0个

________．

Answer 1

无数个；1个；无数个；3个

分析：①θ=60°，由于E、F在菱形的边上，那么在线段AB、AD上，只要EF∥BD，那么所有的E、F点都符合要求，因此这种情况下有无数个符合条件的正三角形．
②60°＜θ＜120°时，若△AEF是正三角形，那么E、F必须在BC、CD上，且关于AC对称，因此满足条件的正三角形只有一个．
③θ=120°时，那么E、F必在线段BC、CD上，连接AC，只要符合△AEC≌△AFB，那么E、F就符合要求，因此符合这样条件的E、F点有无数个，故符合条件的正三角形也由无数个．
④当120°＜θ＜180°时，那么有三种情况：
一、E在AB上，F在BC上，由于∠BAC＞60°，因此这种情况下存在一个符合条件的正三角形；
二、E、F分别在BC、CD上，同②可知这种情况下只有一种符合条件的正三角形；
三、E在CD上，F在AD上，情况同一．
因此当120°＜θ＜180°时，共有3个符合条件的正三角形．
解答：填表如下：

满足的条件	0°＜θ＜60°	θ=60°	60°＜θ＜120°	θ=120°	120°＜θ＜180°
内接正△AEF个数	0个	无数个	1个	无数个	3个

如图：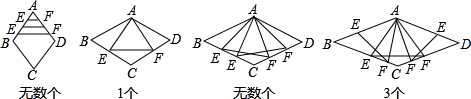

点评：此题主要考查了菱形的性质以及等边三角形的判定和性质，难度适中．