题目内容
 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=34°,则∠C=________.
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=34°,则∠C=________.
28°
分析:连接OB,根据切线的性质得到OB⊥AB,求出∠OBA=90°,根据三角形的内角和定理求出∠AOB的度数,由∠C和∠AOB是同弧所对的圆周角和圆心角,根据圆周角定理即可求出∠C.
解答: 解:连接OB,
解:连接OB,
∵AB切圆O于B,
∴OB⊥AB,
∴∠OBA=90°,
∵∠A=34°,
∴∠AOB=180°-∠A-∠OBA=56°,
∵∠C和∠AOB是同弧所对的圆周角和圆心角,
∴∠C= ∠AOB=28°.
∠AOB=28°.
故答案为:28°.
点评:本题主要考查对三角形的内角和定理,垂线的定义,圆周角定理,切线的性质等知识点的理解和掌握,能灵活运用切线的性质和圆周角定理进行推理是解此题的关键.
分析:连接OB,根据切线的性质得到OB⊥AB,求出∠OBA=90°,根据三角形的内角和定理求出∠AOB的度数,由∠C和∠AOB是同弧所对的圆周角和圆心角,根据圆周角定理即可求出∠C.
解答:
 解:连接OB,
解:连接OB,∵AB切圆O于B,
∴OB⊥AB,
∴∠OBA=90°,
∵∠A=34°,
∴∠AOB=180°-∠A-∠OBA=56°,
∵∠C和∠AOB是同弧所对的圆周角和圆心角,
∴∠C=
 ∠AOB=28°.
∠AOB=28°.故答案为:28°.
点评:本题主要考查对三角形的内角和定理,垂线的定义,圆周角定理,切线的性质等知识点的理解和掌握,能灵活运用切线的性质和圆周角定理进行推理是解此题的关键.

练习册系列答案
相关题目

 9、如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C=
9、如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C=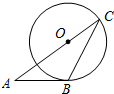 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=48°,则∠C=
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=48°,则∠C= 已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.则sinA的值是
已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.则sinA的值是 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°,则∠C=
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°,则∠C=