题目内容
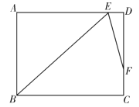
【题目】在矩形![]() 中,
中,![]() 的角平分线
的角平分线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 的角平分线
的角平分线![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
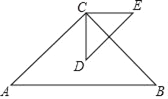
先延长EF和BC,交于点G,再根据条件可以判断三角形ABE为等腰直角三角形,并求得其斜边BE的长,然后根据条件判断三角形BEG为等腰三角形,最后根据△EFD∽△GFC得出CG与DE的倍数关系,并根据BG=BC+CG进行计算即可.
延长EF和BC,交于点G,
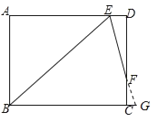
∵3DF=4FC,
∴![]() ,
,
∵矩形ABCD中,∠ABC的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=7,
∴直角三角形ABE中,BE=![]() ,
,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF,
∵AD∥BC,
∴∠G=∠DEF,
∴∠BEG=∠G,
∴BG=BE=![]() ,
,
∵∠G=∠DEF,∠EFD=∠GFC,
∴△EFD∽△GFC,
∴![]() ,
,
设CG=3x,DE=4x,则AD=7+4x=BC,
∵BG=BC+CG,
∴7+4x+3x=7![]() ,
,
解得x=![]() 1,
1,
∴BC=7+4x=7+4![]() 4=3+4
4=3+4![]() ,
,
故选:D.

练习册系列答案
相关题目