题目内容
8.观察以下5个乘法算式:6×10;8×18;11×29;12×26;25×37.(1)请仿照式子“6×34=202-142”,将以上各乘法算式分别写成两数平方差的形式;
(2)如果将上面五个乘法算式的两个因数分别用字母a,b表示(a,b为正数且a<b),请写出ab、b+a、b-a之间的关系式.(只要求写出结果)
分析 (1)观察式子6×34=202-142,发现202${=(\frac{6+34}{2})}^{2}$,142=(34-20)2,由此可得结果;
(2)利用平方差公式和完全平方公式可得结果.
解答 解:(1)∵6×34=202-142,202${=(\frac{6+34}{2})}^{2}$,142=(34-20)2,
∴6×10=${(\frac{6+10}{2})}^{2}$-${(10-\frac{6+10}{2})}^{2}$=82-22;
同理可得:8×18=132-52;11×29=202-92;12×26=192-72;25×37=312-62;
(2)∵(b+a)2=b2+2ab+b2,(b-a)2=b2-2ab+a2,
∴(b+a)2-(b-a)2=4ab.
点评 本题主要考查了数字的变化规律和完全平方公式,通过观察发现规律是解答此题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
18.若函数$y=\frac{m}{x}$的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )
| A. | m>1 | B. | m>0 | C. | m<1 | D. | m<0 |
19.已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是( )
| A. | sinA=$\frac{2}{3}$ | B. | cosA=$\frac{2}{3}$ | C. | tanA=$\frac{2}{3}$ | D. | cotA=$\frac{2}{3}$ |
16.某商品降低x%后是a元,则原价是( )
| A. | a•x%元 | B. | a(1+x%)元 | C. | $\frac{a}{x%}$元 | D. | $\frac{a}{1-x%}$元 |
20.巡道员沿东西方向的铁路进行巡视维护,他从驻地出发,先向东行走7km,休息之后继续向东行走2km,然后折返向西行走12.5km,用有理数的相关知识回答;此时他在驻地的什么方向?与驻地的距离是多少?
17.将边长为1的正方形纸片如图1所示的方法进行对折,记第一次对折后得到的图形面积为 S1,第2次对折后得到的图形面积为S2…,第n次对折后得到的图形面积为Sn,请根据图2化简S1+S2+S3…S2014=( )
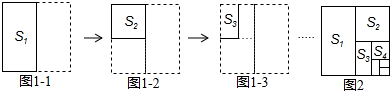

| A. | 1-$\frac{1}{{{2^{2015}}}}$ | B. | $\frac{2014}{2015}$ | C. | 1-$\frac{1}{{{2^{2014}}}}$ | D. | $\frac{2013}{2014}$ |
 某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.
某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.