题目内容
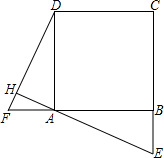
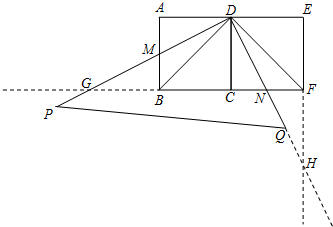
如图,分别延长正方形ABCD的边CB和BA,至点E和点F,使BE=AF,连接EA,并延长交DF于 点H.
点H.
(1)求证:△ADH∽△AEB;
(2)设正方形ABCD的边长为a,BE=b,求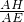 .
.
(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAF=∠ABE=90°,
而BE=AF,
∴△FAD≌△EBA,
∴∠BAE=∠FDA,
又∠BAE=∠HAF,
∴∠HAF=∠FDA,
而∠DAH+∠HAF=90°,
∴∠ADH+∠DAH=90°,
∴∠AHD=90°,
∴△ADH∽△AEB;
(2)解:∵△FAD≌△EBA,
∴AE=DF,
而正方形ABCD的边长为a,BE=b,
∴AF=b,AD=a,
∴DF= =
= ,
,
而S△AFD= AF•AD=
AF•AD= AH•DF,
AH•DF,
∴AH= =
=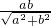 ,
,
∴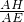 =
=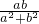 .
.
分析:(1)首先利用已知条件证明△FAD≌△EBA,然后利用全等三角形的性质证明△ADH∽△AEB;
(2)利用(1)可以证明△ADF∽△HAF,然后利用三角形的面积公式和勾股定理即可求解.
点评:此题主要考查了全等三角形、相似三角形的性质与判定及正方形的性质,同时也利用了勾股定理和三角形的面积公式,综合性比较强.
∴AD=AB,∠DAF=∠ABE=90°,
而BE=AF,
∴△FAD≌△EBA,
∴∠BAE=∠FDA,
又∠BAE=∠HAF,
∴∠HAF=∠FDA,
而∠DAH+∠HAF=90°,
∴∠ADH+∠DAH=90°,
∴∠AHD=90°,
∴△ADH∽△AEB;
(2)解:∵△FAD≌△EBA,
∴AE=DF,
而正方形ABCD的边长为a,BE=b,
∴AF=b,AD=a,
∴DF=
 =
= ,
,而S△AFD=
 AF•AD=
AF•AD= AH•DF,
AH•DF,∴AH=
 =
=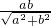 ,
,∴
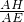 =
=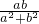 .
.分析:(1)首先利用已知条件证明△FAD≌△EBA,然后利用全等三角形的性质证明△ADH∽△AEB;
(2)利用(1)可以证明△ADF∽△HAF,然后利用三角形的面积公式和勾股定理即可求解.
点评:此题主要考查了全等三角形、相似三角形的性质与判定及正方形的性质,同时也利用了勾股定理和三角形的面积公式,综合性比较强.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 点H.
点H.
 将正方形ABCD的各边按如图所示延长,从射线AB开始,分别在各射线上标记点A1、A2、A3、…,按此规律,点A20在射线
将正方形ABCD的各边按如图所示延长,从射线AB开始,分别在各射线上标记点A1、A2、A3、…,按此规律,点A20在射线