题目内容
(2013•萝岗区一模)如图1,四边形ABHC,ADEF都是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G,设BG交AC于点M.
①求证:BD⊥CF;
②当AB=4,AD=
时,求线段BG的长.

(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G,设BG交AC于点M.
①求证:BD⊥CF;
②当AB=4,AD=
| 2 |

分析:(1)根据正方形性质得出AB=AC,AD=AF,∠BAC=∠DAF=90°,求出∠BAD=∠CAF,根据SAS证出B≌△FAC即可.
(2)①根据全等三角形的性质得出∠FCA=∠DBA,求出∠CMG+∠FCA=∠DBA+∠BMA=90°,求出∠CGM的度数即可.
②过点F作FN⊥AC于点N,求出FN=AN=
AE=1,AE=2,连接BC,求出CN=3,BC=4
,根据tan∠ABM=tan∠FCN=
求出AM=
AB=
,求出BM,求出CM,证△BMA∽△CMG,得出
=
,求出CG,根据勾股定理求出即可.
(2)①根据全等三角形的性质得出∠FCA=∠DBA,求出∠CMG+∠FCA=∠DBA+∠BMA=90°,求出∠CGM的度数即可.
②过点F作FN⊥AC于点N,求出FN=AN=
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| BM |
| AB |
| CM |
| CG |
解答:解:(1)BD=CF成立,
理由是:∵四边形ABHC和四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∴∠BAC-∠DAC=∠DAF-∠DAC,
∴∠BAD=∠CAF,
在△DAB和△FAC中
∴△DAB≌△FAC(SAS),
∴BD=CF.
(2)①证明:∵△DAB≌△FAC,
∴∠FCA=∠DBA,
∵∠CMG=∠BMA,∠CAB=90°,
∴∠CMG+∠FCA=∠DBA+∠BMA=180°-∠CAB=90°,
∴在△CGM中,∠CGM=180°-90°=90°,
∴BD⊥CF.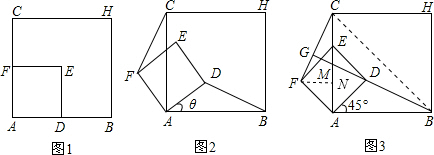
②解:过点F作FN⊥AC于点N,
∵在正方形ADEF中,AD=
=AF,∠DAB=45°,
∴∠DAC=45°,∠FAN=45°,
∵FN⊥AC,
∴∠FNA=90°,
∴∠NFA=45°=∠FAN,
∴FN=AN,
∵四边形ADEF是正方形,
∴AD=AF=EF=
,∠EFA=90°,
∴由勾股定理得:AE=2,
∴FN=AN=1,
连接BC,在等腰直角三角形ABC中,AB=AC=4,
则CN=4-1=3,BC=
=4
,
即在Rt△FCN中,tan∠FCN=
=
,
在Rt△ABM中,tan∠ABM=tan∠FCN=
,
∴AM=
AB=
,
在Rt△BAM中,由勾股定理得:BM=
=
=
,
CM=AC-AM=4-
=
,
∵∠CMG=∠BMA,∠FCA=∠DBA,
∴△BMA∽△CMG,
∴
=
,
∴
=
,
∴CG=
,
在Rt△BGC中,BG=
=
.
理由是:∵四边形ABHC和四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∴∠BAC-∠DAC=∠DAF-∠DAC,
∴∠BAD=∠CAF,
在△DAB和△FAC中
|
∴△DAB≌△FAC(SAS),
∴BD=CF.
(2)①证明:∵△DAB≌△FAC,
∴∠FCA=∠DBA,
∵∠CMG=∠BMA,∠CAB=90°,
∴∠CMG+∠FCA=∠DBA+∠BMA=180°-∠CAB=90°,
∴在△CGM中,∠CGM=180°-90°=90°,
∴BD⊥CF.

②解:过点F作FN⊥AC于点N,
∵在正方形ADEF中,AD=
| 2 |
∴∠DAC=45°,∠FAN=45°,
∵FN⊥AC,
∴∠FNA=90°,
∴∠NFA=45°=∠FAN,
∴FN=AN,
∵四边形ADEF是正方形,
∴AD=AF=EF=
| 2 |
∴由勾股定理得:AE=2,
∴FN=AN=1,
连接BC,在等腰直角三角形ABC中,AB=AC=4,
则CN=4-1=3,BC=
| AC2+AB2 |
| 2 |
即在Rt△FCN中,tan∠FCN=
| FN |
| CN |
| 1 |
| 3 |
在Rt△ABM中,tan∠ABM=tan∠FCN=
| 1 |
| 3 |
∴AM=
| 1 |
| 3 |
| 4 |
| 3 |
在Rt△BAM中,由勾股定理得:BM=
| AB2+AM2 |
42+(
|
4
| ||
| 3 |
CM=AC-AM=4-
| 4 |
| 3 |
| 8 |
| 3 |
∵∠CMG=∠BMA,∠FCA=∠DBA,
∴△BMA∽△CMG,
∴
| BM |
| AB |
| CM |
| CG |
∴
| ||||
| 4 |
| ||
| CG |
∴CG=
4
| ||
| 5 |
在Rt△BGC中,BG=
| BC2-CG2 |
8
| ||
| 5 |
点评:本题考查了正方形的性质,全等三角形的性质和判定,勾股定理,相似三角形的性质和判定的应用,主要考查学生综合运用定理进行推理的能力.

练习册系列答案
相关题目
 (2013•萝岗区一模)解不等式组:
(2013•萝岗区一模)解不等式组: