题目内容
 如图,直线a∥b,那么∠x的度数是________.
如图,直线a∥b,那么∠x的度数是________.
72°
分析:过A作AE∥a,过B作BF∥a,过C作CR∥a,推出直线a∥b∥AE∥BF∥CR,根据平行线的性质推出∠RCT=∠CTZ=30°,求出∠RCB=∠CBF=18°,求出∠ABF=12°=∠EAB,进一步求出∠YWA=180°-∠QWY=60°=∠WAE,根据x=∠WAE+∠EAB即可求出答案.
解答: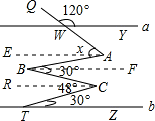 解:过A作AE∥a,过B作BF∥a,过C作CR∥a,
解:过A作AE∥a,过B作BF∥a,过C作CR∥a,
∵直线a∥b,
∴直线a∥b∥AE∥BF∥CR,
∴∠RCT=∠CTZ=30°,
∵∠BCT=48°,
∴∠BCR=48°-30°=18°,
∴∠RCB=∠CBF=18°,
∴∠ABF=30°-18°=12°=∠EAB,
∵∠QWY=120°,
∴∠YWA=180°-∠QWY=60°,
∴∠WAE=∠YWA=60°,
∴x=∠WAE+∠EAB=60°+12°=72°,
故答案为:72°.
点评:本题主要考查对平行线的性质平行公理及推论,邻补角的定义等知识点的理解和掌握,正确作辅助线并灵活运用性质进行推理是解此题的关键.
分析:过A作AE∥a,过B作BF∥a,过C作CR∥a,推出直线a∥b∥AE∥BF∥CR,根据平行线的性质推出∠RCT=∠CTZ=30°,求出∠RCB=∠CBF=18°,求出∠ABF=12°=∠EAB,进一步求出∠YWA=180°-∠QWY=60°=∠WAE,根据x=∠WAE+∠EAB即可求出答案.
解答:
 解:过A作AE∥a,过B作BF∥a,过C作CR∥a,
解:过A作AE∥a,过B作BF∥a,过C作CR∥a,∵直线a∥b,
∴直线a∥b∥AE∥BF∥CR,
∴∠RCT=∠CTZ=30°,
∵∠BCT=48°,
∴∠BCR=48°-30°=18°,
∴∠RCB=∠CBF=18°,
∴∠ABF=30°-18°=12°=∠EAB,
∵∠QWY=120°,
∴∠YWA=180°-∠QWY=60°,
∴∠WAE=∠YWA=60°,
∴x=∠WAE+∠EAB=60°+12°=72°,
故答案为:72°.
点评:本题主要考查对平行线的性质平行公理及推论,邻补角的定义等知识点的理解和掌握,正确作辅助线并灵活运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
 如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2
如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2 如图,已知直线AB∥CD,HL∥FG,EF⊥CD,∠1=40°,那∠EHL的度数为
如图,已知直线AB∥CD,HL∥FG,EF⊥CD,∠1=40°,那∠EHL的度数为








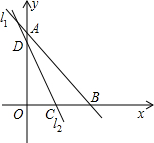 如图,直线l1过A(0,2),B(2,0)两点,直线l2:y=mx+b过点(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.
如图,直线l1过A(0,2),B(2,0)两点,直线l2:y=mx+b过点(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.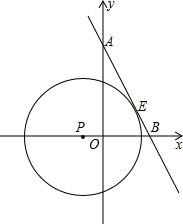 如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2
如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2 ),B(2,0),以P(-
),B(2,0),以P(- ,0)为圆心的圆与直线AB相切于点E.
,0)为圆心的圆与直线AB相切于点E.