题目内容
 已知正比例函数y=x和反比例函数
已知正比例函数y=x和反比例函数 的图象都经过点A(3,3).
的图象都经过点A(3,3).
(1)求反比例函数的解析式;
(2)将直线OA绕点O顺时针旋转得到直线l,当直线l过点B(3, )时,求∠AOB的度数;
)时,求∠AOB的度数;
(3)点P在y轴上,若△AOP是等腰三角形,请直接写出P点的坐标.
 解:(1)将A(3,3)代入反比例函数解析式得:k=9,
解:(1)将A(3,3)代入反比例函数解析式得:k=9,∴y=
 ;
;(2)∵正比例函数y=x,直线l:y=
 x,
x,∴正比例函数倾斜角为45°,直线l倾斜角为30°,
∴∠AOB=15°;
(3)作出线段OA的垂直平分线,与y轴交于P1点,
∵A(3,3),
∴OA=3
 ,
,∵∠AOP1=45°,
∴OP1=
 ×
× =3,即P1(0,3);
=3,即P1(0,3);以A为圆心,OA长为半径画弧,与y轴交于两点,即为点P2与P3;,
过A作AC⊥y轴,以y轴交于C点,可得出AC=OC=3,
∴P2C=OC=3,即OP2=6,
∴P2(0,6);
∵OA=OP3=3
 ,
,∴P3(0,-3
 ).
).综上,满足题意P的坐标为(0,3)或(0,6)或(0,-3
 ).
).分析:(1)将A坐标代入反比例解析式求出k的值,确定出反比例函数解析式;
(2)求出直线OA的倾斜角,以及直线l的倾斜角,相减即可求出∠AOB的度数;
(3)以A为圆心,OA长为半径画弧,与y轴交于两点,即为点P;做出选段OA的垂直平分线,与y轴交于P点,写出所有满足题意P的坐标即可.
点评:此题考查了反比例综合题,涉及的知识有:坐标与图形性质,线段垂直平分线,直线的倾斜角,以及待定系数法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象有一个交点的坐标为(-2,-1),则它的另一个交点的坐标是( )
| k2 |
| x |
| A、(2,1) |
| B、(-2,-1) |
| C、(-2,1) |
| D、(2,-1) |
 横坐标为2.
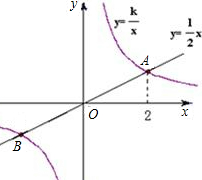
横坐标为2. 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).