题目内容
 如图,直线l过等腰直角三角形ABC顶点B,A、C两点到直线l的距离分别是2和3,则AC的长是
如图,直线l过等腰直角三角形ABC顶点B,A、C两点到直线l的距离分别是2和3,则AC的长是考点:全等三角形的判定与性质,勾股定理,等腰直角三角形
专题:计算题
分析:由三角形ABC为等腰直角三角形,得到∠ABC=90°,AB=BC,利用邻补角定义得到一对角互余,再由AD垂直于DB,利用直角三角形两锐角互余得到一对角互余,利用同角的余角相等得到一对角相等,再由一对直角相等,且AB=BC,利用AAS得到三角形ABD与三角形BCE全等,利用全等三角形对应边相等得到BE=AD=2,DB=CE=3,在直角三角形BCE中,利用勾股定理求出BC的长,即可确定出AC的长.
解答: 解:∵△ABC为等腰直角三角形,
解:∵△ABC为等腰直角三角形,
∴∠ABC=90°,AB=BC,
∴∠ABD+∠EBC=90°,
∵∠ABD+∠BAD=90°,
∴∠EBC=∠BAD,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(AAS),
∴BE=AD=2,DB=CE=3,
在Rt△BCE中,根据勾股定理得:BC=
=
,
在Rt△ABC中,AC=
BC=
.
故答案为:
.
 解:∵△ABC为等腰直角三角形,
解:∵△ABC为等腰直角三角形,∴∠ABC=90°,AB=BC,
∴∠ABD+∠EBC=90°,
∵∠ABD+∠BAD=90°,
∴∠EBC=∠BAD,
在△ABD和△BCE中,
|
∴△ABD≌△BCE(AAS),
∴BE=AD=2,DB=CE=3,
在Rt△BCE中,根据勾股定理得:BC=
| 22+32 |
| 13 |
在Rt△ABC中,AC=
| 2 |
| 26 |
故答案为:
| 26 |
点评:此题考查了全等三角形的判定与性质,勾股定理,以及等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列计算正确的是( )
| A、x+x=x2 |
| B、(x2)3=x5 |
| C、x2•x=x3 |
| D、x6÷x3=x2 |
2014年中考已经结束,市教科研所随机抽取1000名学生试卷进行调查分析,这个问题的样本是( )
| A、1000 |
| B、1000名 |
| C、1000名考生的数学试卷 |
| D、1000名学生 |
计算-3a2(4a-3)等于( )
| A、-12a3+9a2 |
| B、-12a2+9a2 |
| C、-12a3-9a2 |
| D、-12a2-9a2 |
数据2,4,4,5,7的中位数是( )
| A、2 | B、4 | C、5 | D、7 |
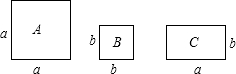 如图,已知正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼成一个长为(a+2b)、宽为(a+b)的大长方形,则需要A类卡片
如图,已知正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼成一个长为(a+2b)、宽为(a+b)的大长方形,则需要A类卡片 如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有
如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有