题目内容
2.求一个一元二次方程x2+7x-1=0,使它的两根分别是方程x2-7x-1=0各根的倒数.分析 设方程x2-7x-1=0的两根为α、β,由根与系数的关系可得出α+β=7,α•β=-1,求出$\frac{1}{α}+\frac{1}{β}$和$\frac{1}{α}•\frac{1}{β}$的值,利用根与系数的关系即可得出结论.
解答 解:设方程x2-7x-1=0的两根为α、β,
则有:α+β=7,α•β=-1.
∴$\frac{1}{α}+\frac{1}{β}$=$\frac{α+β}{α•β}$=-7,$\frac{1}{α}•\frac{1}{β}$=-1,
∴以$\frac{1}{α}$、$\frac{1}{β}$为根的方程为x2+7x-1=0.
故答案为:x2+7x-1=0.
点评 本题考查了根与系数的关系,解题的关键是找出α+β=7,α•β=-1.本题属于基础题,难度不大,解决该题型题目时,根据方程的系数结合根与系数的关系得出两根之和与两根之积是关键.

练习册系列答案
相关题目
12.陆地上最高处是珠穆朗玛峰顶,高出海平面8844m,记为+8844m;陆地上最低处是地处亚洲西部的死海,低于海平面约415m,记为( )
| A. | +415 m | B. | -415 m | C. | ±415 m | D. | -8848 m |
13.等腰三角形的底边BC=8cm,且|AC-BC|=2cm,则腰长AC的长为( )
| A. | 10cm或6cm | B. | 10cm | C. | 6cm | D. | 8cm或6cm |
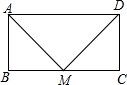 如图所示,矩形ABCD中,M是BC的中点,且MA⊥MD,若矩形的周长为36cm,求此矩形的面积.
如图所示,矩形ABCD中,M是BC的中点,且MA⊥MD,若矩形的周长为36cm,求此矩形的面积. 如图①②都是6×6的正方形网格,△ABC是格点三角形(顶点在格点上).
如图①②都是6×6的正方形网格,△ABC是格点三角形(顶点在格点上). 如图,抛物线y=a(x-2)2+k与x轴交于A,B两点,与y轴的负半轴交于C点,A(1,0),S△ABC=3
如图,抛物线y=a(x-2)2+k与x轴交于A,B两点,与y轴的负半轴交于C点,A(1,0),S△ABC=3