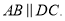��Ŀ����
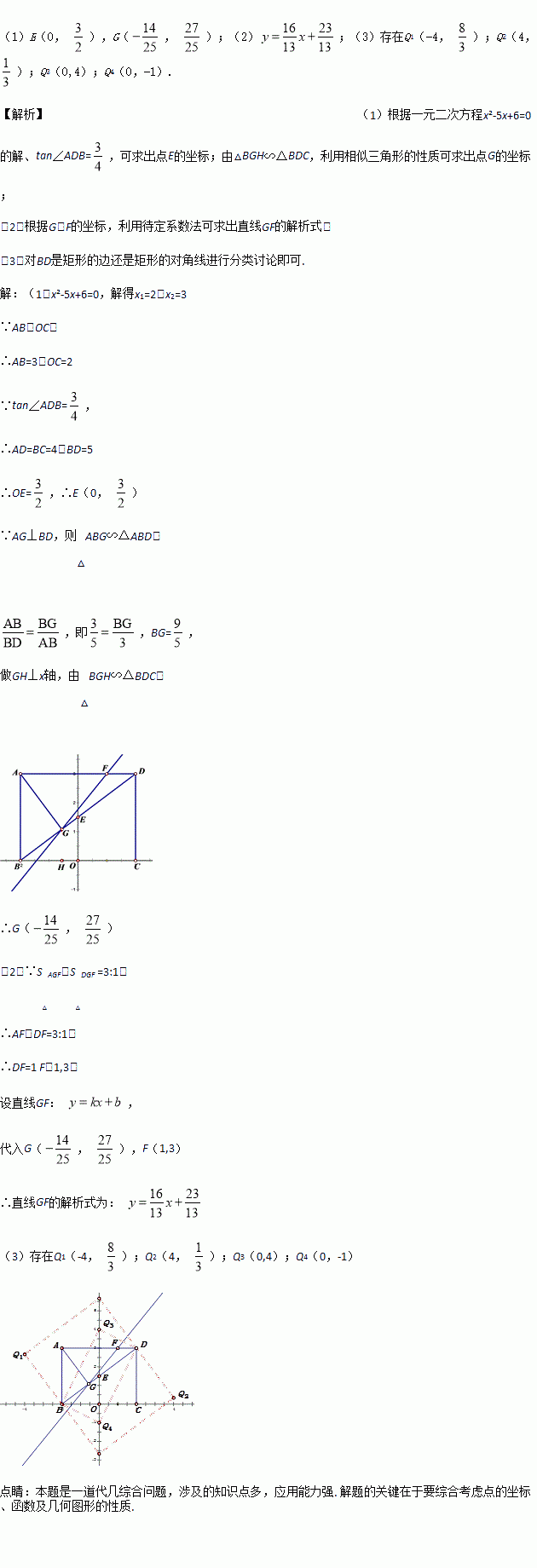
��ͼ������ABCD�ı�BC��x���غϣ����ӶԽ���BD��y���ڵ�E������A��AG��BD�ڵ�G��ֱ��GF��AD�ڵ�F��AB��OC�ij��ֱ���һԪ���η���x²-5x+6=0��������AB��OC������tan��ADB=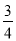 .
.
��1�����E����G�����ꣻ
��2��ֱ��GF�֡�AGDΪ��AGF���DGF���������Σ���S��AGF��S��DGF =3:1����ֱ��GF�Ľ���ʽ��
��3����P��y���ϣ�������ƽ�����Ƿ����һ��Q��ʹ�Ե�B��D��P��QΪ������ı����Ǿ��Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵������.
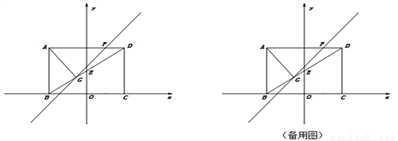
��ϰ��ϵ�д�
�����Ŀ

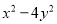 �ֽ���ʽ�Ľ���ǣ� ��
�ֽ���ʽ�Ľ���ǣ� ��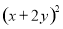 B.
B. 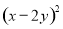 C.
C. 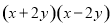 D.
D. 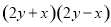
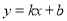 ��
��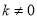 ������˵��y��x�������������˵��b<0�����������������ͼ���ǣ� ��
������˵��y��x�������������˵��b<0�����������������ͼ���ǣ� ��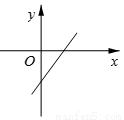 B.
B. 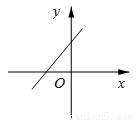
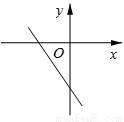 D.
D. 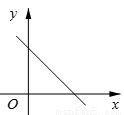
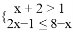 ������������________��
������������________��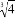 B.
B.  C.
C. 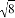 D. 3.14159
D. 3.14159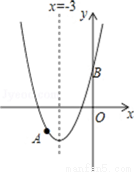
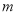 �Ƿ���
�Ƿ���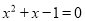 �ĸ�����ʽ��
�ĸ�����ʽ��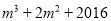 ��ֵΪ_______________.
��ֵΪ_______________.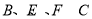 ������ͬһ��ֱ���ϣ�
������ͬһ��ֱ���ϣ� 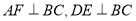 ������ֱ�Ϊ
������ֱ�Ϊ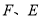 ����
����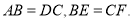 ��˵��
��˵��