题目内容
4.小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.妈妈说:“今天买这两样菜共花了45元,上月买同重量的这两种菜只要36元”;爸爸说:“报纸上说了萝卜的单价上涨50%,排骨单价上涨20%”;小明说:爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?请你通过列一元一次方程求解这天萝卜、排骨的单价(单位:元/斤).
分析 设上月萝卜的单价是x元/斤,则排骨的单价$\frac{36-3x}{2}$元/斤,根据小明的爸爸和妈妈的对话找到等量关系列出方程求解即可.
解答 解:设上月萝卜的单价是x元/斤,则排骨的单价$\frac{36-3x}{2}$元/斤,根据题意得
3(1+50%)x+2(1+20%)($\frac{36-3x}{2}$)=45,
解得x=2,
则$\frac{36-3x}{2}$=$\frac{36-3×2}{2}$=15.
所以这天萝卜的单价是(1+50%)×2=3(元/斤),
这天排骨的单价是(1+20%)×15=(1+20%)×15=18(元/斤).
答:这天萝卜的单价是3元/斤,排骨的单价是18元/斤.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
12.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x-3=0}\\{3x-2y=7}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-y=3}\\{3xy=8}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=3}\\{x-z=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{3}{y}=4}\\{\frac{1}{3}x+\frac{1}{2}y=1}\end{array}\right.$ |
9.为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的,该市自来水收费价格见表,例如:某户居民1月份用水15立方米,则应收水费:2×10+3×(15-10)=35(元).
(1)若该户居民2月份用水24立方米,则应收水费多少元?
(2)若该户居民3、4月份共用水26立方米(3月份用水量不超过10立方米),共交水费60元,则该户居民3、4月份各用水多少立方米?
| 每月用水量 | 单价 |
| 不超出10立方米的部分 | 2元/立方米 |
| 超出10立方米不超出20立方米部分 | 3元/立方米 |
| 超出20立方米的部分 | 4元/立方米 |
(2)若该户居民3、4月份共用水26立方米(3月份用水量不超过10立方米),共交水费60元,则该户居民3、4月份各用水多少立方米?
16.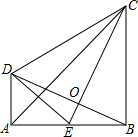 如图,CB⊥AB,DA⊥AB,垂足分别是A、B,AB=BC,E是AB中点,CE⊥DB,CE交BD于点O.下列结论:①BE=AD;②AC垂直平分DE;③∠DBC=∠DCB;④∠CED=∠DBC;⑤BC=CD.其中正确的有( )
如图,CB⊥AB,DA⊥AB,垂足分别是A、B,AB=BC,E是AB中点,CE⊥DB,CE交BD于点O.下列结论:①BE=AD;②AC垂直平分DE;③∠DBC=∠DCB;④∠CED=∠DBC;⑤BC=CD.其中正确的有( )
 如图,CB⊥AB,DA⊥AB,垂足分别是A、B,AB=BC,E是AB中点,CE⊥DB,CE交BD于点O.下列结论:①BE=AD;②AC垂直平分DE;③∠DBC=∠DCB;④∠CED=∠DBC;⑤BC=CD.其中正确的有( )
如图,CB⊥AB,DA⊥AB,垂足分别是A、B,AB=BC,E是AB中点,CE⊥DB,CE交BD于点O.下列结论:①BE=AD;②AC垂直平分DE;③∠DBC=∠DCB;④∠CED=∠DBC;⑤BC=CD.其中正确的有( )| A. | ①②③ | B. | ①③⑤ | C. | ①②④ | D. | ②③⑤ |
13.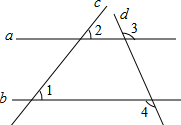 如图,若∠1=40°,∠2=40°,∠3=110°36′,则∠4的度数为( )
如图,若∠1=40°,∠2=40°,∠3=110°36′,则∠4的度数为( )
 如图,若∠1=40°,∠2=40°,∠3=110°36′,则∠4的度数为( )
如图,若∠1=40°,∠2=40°,∠3=110°36′,则∠4的度数为( )| A. | 68.6° | B. | 110°36′ | C. | 68.4° | D. | 69.4° |
 如图,有长为24cm的篱笆,一面利用墙(墙长10m)围成中间隔道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为y(m2).
如图,有长为24cm的篱笆,一面利用墙(墙长10m)围成中间隔道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为y(m2).