Question

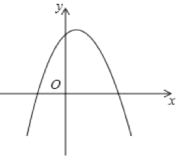
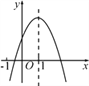
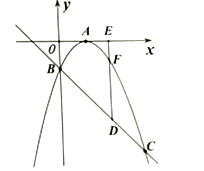
【题目】如图，已知二次函数的图象顶点在轴上，且，与一次函数的图象交于轴上一点和另一交点.

求抛物线的解析式；

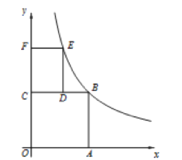
点为线段上一点，过点作轴，垂足为，交抛物线于点，请求出线段的最大值.

Answer 1

【答案】(1) ；（2）线段的最大值为.

【解析】

（1）根据题意首先计算A、B点的坐标，设出二次函数的解析式，代入求出参数即可.

（2）根据题意设F点的横坐标为m,再结合抛物线和一次函数的解析式即可表示F、D的纵坐标，所以可得DF的长度，使用配方法求解出最大值即可.

解：，二次函数与一次函数的图象交于轴上一点，

点为，点为.

二次函数的图象顶点在轴上.

设二次函数解析式为.

把点代入得，

.

抛物线的解析式为，即.

设点坐标为，点坐标为.

.

当时，即，解得.

点为线段上一点,

.

当时，线段的最大值为.