题目内容
 如图,点A在双曲线y=
如图,点A在双曲线y=| 3 |
| x |
| k |
| x |
考点:相似三角形的判定与性质,反比例函数图象上点的坐标特征
专题:
分析:根据题意得出△OBC∽△AOD,则
=
=
,进而求出
=
=
=
,再利用k=xy=-
b×
a=-
ab得出即可.
| BC |
| DO |
| CO |
| AD |
| BO |
| AO |
| BC |
| DO |
| CO |
| AD |
| BO |
| AO |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
解答: 解:过点B作BC⊥x轴于点C,AD⊥x轴于点D,
解:过点B作BC⊥x轴于点C,AD⊥x轴于点D,
∵OA⊥OB,
∴∠1+∠2=90°,
∵∠1+∠OAD=90°,
∴∠1+∠OAD=90°,
∴∠2=∠OAD,
又∵∠BCO=∠ADO=90°,
∴△OBC∽△AOD,
∴
=
=
,
∵∠BAD=30°,∠BOA=90°,
∴
=
=
=
,
设B(x,y),A(a,b),
∴
=
=
,
∴x=-
b,y=
a,
∵ab=3,
∴k=xy=-
b×
a=-
ab=-1.
故答案为:-1.
 解:过点B作BC⊥x轴于点C,AD⊥x轴于点D,
解:过点B作BC⊥x轴于点C,AD⊥x轴于点D,∵OA⊥OB,
∴∠1+∠2=90°,
∵∠1+∠OAD=90°,
∴∠1+∠OAD=90°,
∴∠2=∠OAD,
又∵∠BCO=∠ADO=90°,
∴△OBC∽△AOD,
∴
| BC |
| DO |
| CO |
| AD |
| BO |
| AO |
∵∠BAD=30°,∠BOA=90°,
∴
| BC |
| DO |
| CO |
| AD |
| BO |
| AO |
| ||
| 3 |
设B(x,y),A(a,b),
∴
| y |
| a |
| -x |
| b |
| ||
| 3 |
∴x=-
| ||
| 3 |
| ||
| 3 |
∵ab=3,
∴k=xy=-
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
故答案为:-1.
点评:此题主要考查了相似三角形的判定与性质以及反比例函数图象上点的坐标性质等知识,得出
=
=
=
是解题关键.
| BC |
| DO |
| CO |
| AD |
| BO |
| AO |
| ||
| 3 |

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,经过一段时间统计,他在路口遇到红灯的概率为
,遇到黄灯的概率为
,那么他遇到绿灯的概率为( )
| 1 |
| 4 |
| 1 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如果某物体的三视图如图,那么该物体的形状是( )
如果某物体的三视图如图,那么该物体的形状是( )| A、正方体 | B、长方体 |
| C、三棱柱 | D、圆锥 |
 如图,点A、B、C、D在⊙O上,且AB∥CD,∠ABC=20°,则∠BOD=
如图,点A、B、C、D在⊙O上,且AB∥CD,∠ABC=20°,则∠BOD=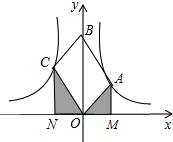 如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=
如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y= 在?ABCD中,点E为AD的中点,连接BE,交AC于点F,AF=3,则AC=
在?ABCD中,点E为AD的中点,连接BE,交AC于点F,AF=3,则AC=