题目内容
已知:如图,二次函数y=a(x+1)2-4的图象与x轴分别交于A、B两点,与y轴交于点D,点C是二次函数y=a(x+1)2-4的图象的顶点,CD=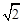 .
.
(1)求a的值.
(2)点M在二次函数y=a(x+1)2-4图象的对称轴上,且∠AMC=∠BDO,求点M的坐标.
(3)将二次函数y=a(x+1)2-4的图象向下平移k(k>0)个单位,平移后的图象与直线CD分别交于E、F两点(点F在点E左侧),设平移后的二次函数的图象的顶点为C1,与y轴的交点为D1,是否存在实数k,使得CF⊥FC1,若存在,求出k的值;若不存在,请说明理由.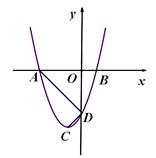
.解:(1)∵C(-1,-4),CD= ,
,
∴D(0,-3)
∴a="1"
∴
即y = x2+2x - 3
(2)M(-1,6)或(-1,-6)
(3)存在
由CC1=DD1=k,CC1∥DD1,
∴∠ F C C1=∠F D D1=45°,
∵CF⊥FC1,∴∠CC1F=45°
即△CFC1为等腰直角三角形,且CC1=k,
∴F(- k-1,-
k-1,- k-4),
k-4),
由点F在新抛物线y=x2+2x-3- k上,
∴ (- k-1)2+2(-
k-1)2+2(- k-1)-3-k =-
k-1)-3-k =- k-4,
k-4,
解得k=2或k=0(舍),
∴k =2.
当k =2时,
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
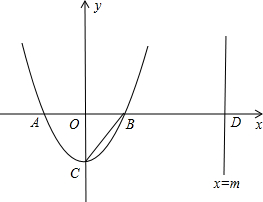 左边),与y轴交于点C.直线x=m(m>2)与x轴交于点D.
左边),与y轴交于点C.直线x=m(m>2)与x轴交于点D. 已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点. 已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:
已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: (2013•闸北区一模)已知:如图,二次函数
(2013•闸北区一模)已知:如图,二次函数 已知:如图,二次函数y=ax2-2ax+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
已知:如图,二次函数y=ax2-2ax+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).