题目内容
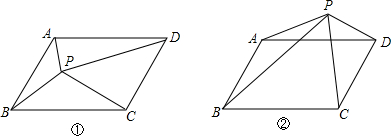
 如图,在?ABCD中,AD=2AB,延长AB至点F,延长BA至点E,使AB=AE=BF,连结EC,FD交于点O.求证:FD⊥EC.
如图,在?ABCD中,AD=2AB,延长AB至点F,延长BA至点E,使AB=AE=BF,连结EC,FD交于点O.求证:FD⊥EC.考点:平行四边形的性质
专题:
分析:连接MN,求出DM=DC=CN,根据菱形的判定推出四边形CNMD是菱形,根据菱形的性质得出即可.
解答:证明:
连接MN,
∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,AB∥CD,
∴△AEM∽△CDM,
∴
=
,
∵AB=AE=BF,AB=CD,
∴AE=CD,
∴AM=DM,
∵AD=2AB,AB=CD,
∴DM=DC,
同理CN=DC,
∴DM∥CN,DM=CN,
∴四边形CNMD是菱形,
∴FD⊥EC.

连接MN,
∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,AB∥CD,
∴△AEM∽△CDM,
∴
| AE |
| CD |
| AM |
| DM |
∵AB=AE=BF,AB=CD,
∴AE=CD,
∴AM=DM,
∵AD=2AB,AB=CD,
∴DM=DC,
同理CN=DC,
∴DM∥CN,DM=CN,
∴四边形CNMD是菱形,
∴FD⊥EC.
点评:本题考查了平行四边形的性质,菱形的性质和判定,相似三角形的性质和判定的应用,注意:菱形的对角线互相垂直.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 圆心角都是90°的扇形OAB与扇形OCD按如图所示的方式叠放在一起,连结AC,BD.若AO=3cm,OC=1cm,求阴影部分的面积.
圆心角都是90°的扇形OAB与扇形OCD按如图所示的方式叠放在一起,连结AC,BD.若AO=3cm,OC=1cm,求阴影部分的面积.
 如图,A,B,C是⊙O上的三个点,连结
如图,A,B,C是⊙O上的三个点,连结
 如图,用20m的篱笆围成一个矩形的花圃.设连墙的一边为x(m),矩形的面积为y(m2).
如图,用20m的篱笆围成一个矩形的花圃.设连墙的一边为x(m),矩形的面积为y(m2).