题目内容
(1)如图①,P是?ABCD内一点,请说明S△PAB,S△PCD,S△PAD,S△PBC间的关系;
(2)如图②,P是?ABCD外一点,请说明S△PAB,S△PCD,S△PBC,S△PAD间的关系.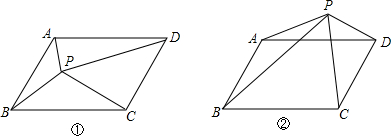
(2)如图②,P是?ABCD外一点,请说明S△PAB,S△PCD,S△PBC,S△PAD间的关系.

考点:平行四边形的性质
专题:
分析:(1)过P作PM⊥BC,PN⊥AD分别于点M、N,则MN就是平行四边形ABCD的高,根据三角形的面积公式以及平行四边形的面积公式即可求解;
(2)过P作PF⊥BC于点F,交AD于点E,根据三角形的面积公式以及(1)中的结论S△PAB+S△PCD=
S平行四边形ABCD即可求解.
(2)过P作PF⊥BC于点F,交AD于点E,根据三角形的面积公式以及(1)中的结论S△PAB+S△PCD=
| 1 |
| 2 |
解答: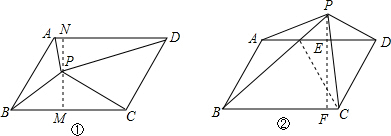 解:(1)过P作PM⊥BC,PN⊥AD分别于点M、N.
解:(1)过P作PM⊥BC,PN⊥AD分别于点M、N.
则MN就是平行四边形ABCD的高.
则S平行四边形ABCD=AD•MN,
∵S△PAD=
AD•PN,
S△PBC=
BC•PM=
AD•PM,
∴S△PAD+S△PBC=
AD•(PM+PN)=
AD•MN=
S平行四边形ABCD.
同理,S△PAB+S△PCD=
S平行四边形ABCD.
则S△PAB+S△PCD=S△PAD+S△PBC;
(2)过P作PF⊥BC于点F,交AD于点E.
∵S△PBC=
BC•PF=
AD•(PE+EF)=
AD•EF+
AD•PE=
S平行四边形ABCD+
AD•PE,
又∵S△PAD=
AD•PE,S△BCE=
S平行四边形ABCD,
同(1)可得S△PAB+S△PCD=
S平行四边形ABCD.
∴S△PBC=S△PAB+S△PCD+S△PAD.
 解:(1)过P作PM⊥BC,PN⊥AD分别于点M、N.
解:(1)过P作PM⊥BC,PN⊥AD分别于点M、N.则MN就是平行四边形ABCD的高.
则S平行四边形ABCD=AD•MN,
∵S△PAD=
| 1 |
| 2 |
S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△PAD+S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
同理,S△PAB+S△PCD=
| 1 |
| 2 |
则S△PAB+S△PCD=S△PAD+S△PBC;
(2)过P作PF⊥BC于点F,交AD于点E.
∵S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵S△PAD=
| 1 |
| 2 |
| 1 |
| 2 |
同(1)可得S△PAB+S△PCD=
| 1 |
| 2 |
∴S△PBC=S△PAB+S△PCD+S△PAD.
点评:本题考查了平行四边形的性质以及三角形的面积公式,正确理解三角形的面积和平行四边形的面积公式,得到S△PAB+S△PCD=
S平行四边形ABCD是关键.
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
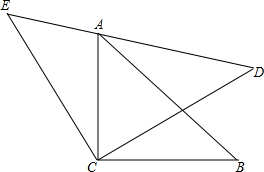 如图,△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2.(提示:连接BD)
如图,△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2.(提示:连接BD)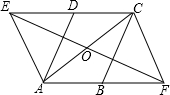 如图,在平行四边形ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.求证:四边形AFCE是平行四边形.
如图,在平行四边形ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.求证:四边形AFCE是平行四边形. 如图,在?ABCD中,AD=2AB,延长AB至点F,延长BA至点E,使AB=AE=BF,连结EC,FD交于点O.求证:FD⊥EC.
如图,在?ABCD中,AD=2AB,延长AB至点F,延长BA至点E,使AB=AE=BF,连结EC,FD交于点O.求证:FD⊥EC.