题目内容
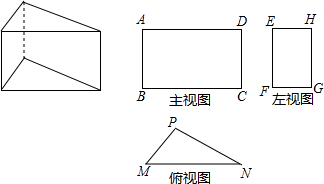 几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=
几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=| 4 |
| 5 |
(1)求BC及FG的长;
(2)若主视图与左视图两矩形相似,求AB的长;
(3)在(2)的情况下,求直三棱柱的表面积.
考点:由三视图判断几何体,相似多边形的性质
专题:
分析:(1)由图可知BC=MN,FG=PM,进一步由锐角三角函数的意义与勾股定理求得答案即可;
(2)利用相似的性质列出比例式,代入数值求得答案即可;
(3)求出五个面的面积和得出答案即可.
(2)利用相似的性质列出比例式,代入数值求得答案即可;
(3)求出五个面的面积和得出答案即可.
解答:解:(1)由图可知:
BC=MN,FG=PM,
∵sin∠PMN=
=
,PN=4,
∴MN=5,
∴FG=PM=
=3;
(2)∵矩形ABCD与矩形EFGH相似,且AB=EF,
∴
=
,
即
=
,
∴AB=
;
(3)直三棱柱的表面积:
×3×4×2+5×
+3×
+4×
=12+12
.
BC=MN,FG=PM,
∵sin∠PMN=
| PN |
| MN |
| 4 |
| 5 |
∴MN=5,
∴FG=PM=
| MN2-PN2 |
(2)∵矩形ABCD与矩形EFGH相似,且AB=EF,
∴
| AB |
| FG |
| BC |
| EF |
即
| AB |
| 3 |
| 5 |
| AB |
∴AB=
| 15 |
(3)直三棱柱的表面积:
| 1 |
| 2 |
| 15 |
| 15 |
| 15 |
| 15 |
点评:此题考查立体图形的三视图,锐角三角函数,相似的性质以及立体图形的表面积,从三视图入手,找出边之间的关系,利用三角函数解决问题.

练习册系列答案
相关题目
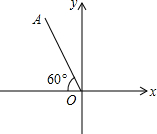 如图,OA=2,OA与x轴负半轴的夹角是60°,点A关于y轴的对称点是点A′,点P是x轴上一动点,当PA+PA′的值最小时,点P的坐标是( )
如图,OA=2,OA与x轴负半轴的夹角是60°,点A关于y轴的对称点是点A′,点P是x轴上一动点,当PA+PA′的值最小时,点P的坐标是( )| A、(-1,0) | ||
| B、(1,0) | ||
| C、(0,0) | ||
D、(
|
 有理数a、b在数轴上的位置如图所示,则a-b的值在( )
有理数a、b在数轴上的位置如图所示,则a-b的值在( )| A、-3与-2之间 |
| B、2与3之间 |
| C、0与1之间 |
| D、-2与-1之间 |
二次函数y=-x2+3的图象的顶点坐标是( )
| A、(0,0) |
| B、(0,3) |
| C、(0,-3) |
| D、(3,0) |
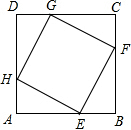 如图,在正方形ABCD中,E,F,G,H分别是边AB,BC,CD,DA上的点,且AE=BF=CG=DH,试判定四边形EFGH的形状,并证明你的结论.
如图,在正方形ABCD中,E,F,G,H分别是边AB,BC,CD,DA上的点,且AE=BF=CG=DH,试判定四边形EFGH的形状,并证明你的结论. 如图,在△ABC中,AB=AC,AC边上的高BD=10,P为边BC上任意一点,PM⊥AB,PN⊥AC,垂足分别是M,M.求PM+PN的值.
如图,在△ABC中,AB=AC,AC边上的高BD=10,P为边BC上任意一点,PM⊥AB,PN⊥AC,垂足分别是M,M.求PM+PN的值.