题目内容
11.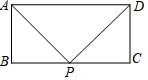 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系式一定满足( )| A. | ${a^2}≥\frac{1}{4}{b^2}$ | B. | a2≥b2 | C. | ${a^2}≥\frac{9}{4}{b^2}$ | D. | a2≥4b2 |
分析 本题可结合方程思想来解答.由于△ABP和△DCP相似,可得出关于AB、PC、BP、CD的比例关系式.设PC=x,那么BP=a-x,根据比例关系式可得出关于x的一元二次方程,由于BC边上至少有一点符合条件的P点,因此方程的△≥0,由此可求出a、b的大小关系.
解答 解:若设PC=x,则BP=a-x,
∵△ABP∽△PCD,
∴$\frac{AB}{PC}$=$\frac{BP}{CD}$,即 $\frac{b}{x}$=$\frac{a-x}{b}$,
即x2-ax+b2=0方程有解的条件是:a2-4b2≥0,
∴a2≥4b2,
故选D.0,
点评 本题考查相似三角形的判定和性质、矩形的性质等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.李克强总理在2017年政府工作报告中指出,扎实推进新型城镇化,深化户籍制度改革,今年实现进城落户1300万人以上,其中1300万用科学记数法表示为( )
| A. | 1.3×107 | B. | 1.3×106 | C. | 0.13×108 | D. | 1.3×108 |
2.下面的图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.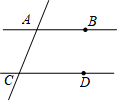 如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α-β,③β-α,④360°-α-β,∠AEC的度数可能是( )
如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α-β,③β-α,④360°-α-β,∠AEC的度数可能是( )
 如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α-β,③β-α,④360°-α-β,∠AEC的度数可能是( )
如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α-β,③β-α,④360°-α-β,∠AEC的度数可能是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
16.在-次射击比赛中,甲乙两运动员分别打了10发,并且经过计算知道甲运动员的10发的方差S2=1.36,乙运动员的10发的方差S2=2.03,那么对于甲乙两运动员的成绩,下列说法正确的是( )
| A. | 甲比乙好 | B. | 乙比甲好 | C. | 甲比乙波动大 | D. | 甲比乙波动小 |
3.下列各式化简结果为有理数的是( )
| A. | $\sqrt{2}$ | B. | ($\sqrt{3}$-1)2 | C. | $\frac{π}{3}$ | D. | $\root{3}{-8}$ |
20.如果把分式$\frac{xy}{2x-y}$中的x和y都扩大3倍,那么分式的值( )
| A. | 不变 | B. | 扩大3倍 | C. | 扩大6倍 | D. | 扩大9倍 |
 如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个实数中,绝对值最大的一个是( )
如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个实数中,绝对值最大的一个是( )