Question

（本题满分10分）将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，如图①，我们将这种变换记为[θ，n]．

（1）如图①，对△ABC作变换[50°，]得△AB′C′，则S△AB′C′：S△ABC= ；直线BC与直线BC′所夹的锐角为 度；

（2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC 作变换[θ，n]得△AB'C'，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ 和n的值；

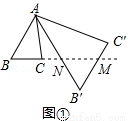
（3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=l，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB'C'为平行四边形，求θ 和n的值．

 

 

Answer 1

（1）5，50；（2）60°，2；（3）72°，．

【解析】

试题分析：（1）由旋转与相似的性质，即可得S△AB′C′：S△ABC=3，然后由△ABN与△B′MN中，∠B=∠B′，∠ANB=∠B′NM，可得∠BMB′=∠BAB′，即可求得直线BC与直线B′C′所夹的锐角的度数；

（2）由四边形 ABB′C′是矩形，可得∠BAC′=90°，然后由θ=∠CAC′=∠BAC′﹣∠BAC，即可求得θ的度数，又由含30°角的直角三角形的性质，即可求得n的值；

（3）由四边形ABB′C′是平行四边形，易求得θ=∠CAC′=∠ACB=72°，又由△ABC∽△B′BA，根据相似三角形的对应边成比例，易得AB2=CB•BB′=CB（BC+CB′），继而求得答案．

试题解析：（1）根据题意得：△ABC∽△AB′C′，∴S△AB′C′：S△ABC=（）2=5，∠B=∠B′，

∵∠ANB=∠B′NM，∴∠BMB′=∠BAB′=50°；故答案为：5，50．

（2）∵四边形 ABB′C′是矩形，∴∠BAC′=90°．∴θ=∠CAC′=∠BAC′﹣∠BAC=90°—30°=60°．

在 Rt△ABC 中，∠ABB'=90°，∠BAB′=60°，∴∠AB′B=30°，∴n=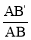=2．

（3）∵四边形ABB′C′是平行四边形，∴AC′∥BB′，

又∵∠BAC=36°，∴θ=∠CAC′=∠ACB=72°．∴∠C′AB′=∠BAC=36°，而∠B=∠B，∴△ABC∽△B′BA，∴AB：BB′=CB：AB，∴AB2=CB•BB′=CB（BC+CB′），

而 CB′=AC=AB=B′C′，BC=1，∴AB2=1（1+AB），∴AB=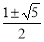．∵AB＞0，∴n=．

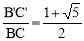考点：1．相似三角形的判定与性质；2．平行四边形的性质；3．矩形的性质；4．旋转的性质．