题目内容
20.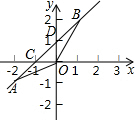 如图,已知一次函数y=kx+b的图象经过A(-2,-1)、B(1,2)两点,并且交x轴于点C,交y轴于点D.
如图,已知一次函数y=kx+b的图象经过A(-2,-1)、B(1,2)两点,并且交x轴于点C,交y轴于点D.(1)求该一次函数的解析式;
(2)求tan∠BAO的值.
分析 (1)将A、B两点坐标代入一次函数y=kx+b即可求得一次函数的解析式;
(2)过O作OM⊥AB于M,由y=x+1,求出C(-1,0),根据三角形的面积公式求出OM=$\frac{\sqrt{2}}{2}$.由互相垂直的两条直线斜率之积为-1可得直线OM的解析式为y=-x,由OM=$\frac{\sqrt{2}}{2}$,求得M点的坐标为($\frac{1}{2}$,-$\frac{1}{2}$),AM=$\frac{\sqrt{26}}{2}$,然后根据正切函数的定义即可求出tan∠BAO=$\frac{OM}{AM}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{26}}{2}}$=$\frac{\sqrt{13}}{13}$.
解答 解:(1)将A(-2,-1),B(1,2)分别代入y=kx+b得$\left\{\begin{array}{l}{-2k+b=-1}\\{k+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$.
所以y=x+1;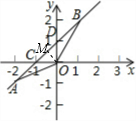 (2)过O作OM⊥AB于M,如图.
(2)过O作OM⊥AB于M,如图.
∵y=x+1,
∴y=0时,x+1=0,x=-1,
∴C(-1,0).
∵S△AOB=S△AOC+S△COB=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×2=1.5,AB=$\sqrt{(1+2)^{2}+(2+1)^{2}}$=3$\sqrt{2}$
∴$\frac{1}{2}$AB•OM=1.5,
∴OM=$\frac{2×1.5}{3\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
过O作OM⊥AB于M,
∵直线AB的解析式为y=x+1,
∴直线OM的解析式为y=-x,
设M点的坐标为(x,-x),则OM=$\sqrt{2}$x,
∴$\sqrt{2}$x=$\frac{\sqrt{2}}{2}$,
∴x=$\frac{1}{2}$,
∴M点的坐标为($\frac{1}{2}$,-$\frac{1}{2}$),
∵A(-2,-1)、
∴AM=$\sqrt{(\frac{1}{2}+2)^{2}+(-\frac{1}{2}+1)^{2}}$=$\frac{\sqrt{26}}{2}$,
∴tan∠BAO=$\frac{OM}{AM}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{26}}{2}}$=$\frac{\sqrt{13}}{13}$.
点评 本题考查了待定系数法求一次函数解析式,一次函数图象上点的坐标特征,三角形的面积,互相垂直的两条直线斜率之积为-1,锐角三角函数的定义,求出M点坐标是解题的关键.

| A. | 23x5的系数是1,次数是8 | B. | 若x2+mx是单项式,则m=0 | ||
| C. | 若-$\frac{2}{3}$xmy3的次数是5,则m=5 | D. | 0不是单项式 |
| A. | y=-x | B. | y=2+3x | C. | y=5x | D. | y=-3+2x |
 如图,点D在AB上,AB=AC,AD=DC=BC,则图中的等腰三角形共有( )
如图,点D在AB上,AB=AC,AD=DC=BC,则图中的等腰三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无法确定 |
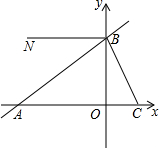 如图,在坐标系中,直线y=-3x+6与x轴的正半轴交于点C,与y轴的正半轴交于点B,直线BA与x轴的负半轴交于点A,AB=5OC,射线BN∥x轴.
如图,在坐标系中,直线y=-3x+6与x轴的正半轴交于点C,与y轴的正半轴交于点B,直线BA与x轴的负半轴交于点A,AB=5OC,射线BN∥x轴.