题目内容
如图,菱形ABCD中,对角线AC、BD交于点O,点P在对角线BD上运动(B、D两点除外),线段PA绕点P顺时针旋转m°(0<m<180),得线段PQ.(1)若点Q与点D重合,请在图中用尺规作出点P所处的位置(不写作法,保留作图痕迹);
(2)若点Q落在边CD上,且∠ADB=n°.
①探究m与n之间的数量关系;
②若点P在线段OB上运动,PQ=QD,求n的取值范围.(在备用图中探究)

【答案】分析:(1)根据垂直平分线的性质和作法作出AD的垂直平分线即可;
(2)①利用旋转的性质得出PC=PQ,再利用菱形的性质得出∠3=∠PAD,进而求出∠PAD+∠PQD=180°,得出即可;
②利用PQ=QD,得出∠PAD=∠PCQ=∠PQC=2∠CDB=2n°,进而利用∠BCD≥∠3≥∠ACD,得出180-2n≥2n≥90-n,求出即可.
解答: 解:(1)如图1所示:作AD的垂直平分线,交BC于点P.
解:(1)如图1所示:作AD的垂直平分线,交BC于点P.
(2)①如图2,连接PC.
由PC=PQ,得∠3=∠4.
由菱形ABCD,得∠3=∠PAD.
所以得∠4=∠PAD,
而∠4+∠PQD=180°.
所以∠PAD+∠PQD=180°.
所以m+2n=180.
②解法一:∵PQ=QD,
∴∠PAD=∠PCQ=∠PQC=2∠CDB=2n°.
而点P在线段BO上运动,
∴∠BCD≥∠3≥∠ACD,
∴180-2n≥2n≥90-n,
∴30≤n≤45.
解法二:由PQ=QD,可得∠QPD=∠1,
又∵∠1=∠2,
∴∠QPD=∠2,
∵点P在线段OB上运动,
∴∠ABC≤∠APQ且∠APQ≤90°+∠2(或∠ABC≤∠APQ≤90°+∠2)
即(2n≤180-2n≤90+n)
∴30≤n≤45.
点评:此题主要考查了垂直平分线的性质和菱形的性质以及外角的性质等知识,熟练利用相关知识得出对应角的关系是解题关键.
(2)①利用旋转的性质得出PC=PQ,再利用菱形的性质得出∠3=∠PAD,进而求出∠PAD+∠PQD=180°,得出即可;
②利用PQ=QD,得出∠PAD=∠PCQ=∠PQC=2∠CDB=2n°,进而利用∠BCD≥∠3≥∠ACD,得出180-2n≥2n≥90-n,求出即可.
解答:
 解:(1)如图1所示:作AD的垂直平分线,交BC于点P.
解:(1)如图1所示:作AD的垂直平分线,交BC于点P.(2)①如图2,连接PC.
由PC=PQ,得∠3=∠4.
由菱形ABCD,得∠3=∠PAD.
所以得∠4=∠PAD,
而∠4+∠PQD=180°.
所以∠PAD+∠PQD=180°.
所以m+2n=180.
②解法一:∵PQ=QD,
∴∠PAD=∠PCQ=∠PQC=2∠CDB=2n°.

而点P在线段BO上运动,
∴∠BCD≥∠3≥∠ACD,
∴180-2n≥2n≥90-n,
∴30≤n≤45.
解法二:由PQ=QD,可得∠QPD=∠1,
又∵∠1=∠2,
∴∠QPD=∠2,
∵点P在线段OB上运动,
∴∠ABC≤∠APQ且∠APQ≤90°+∠2(或∠ABC≤∠APQ≤90°+∠2)
即(2n≤180-2n≤90+n)
∴30≤n≤45.
点评:此题主要考查了垂直平分线的性质和菱形的性质以及外角的性质等知识,熟练利用相关知识得出对应角的关系是解题关键.

练习册系列答案
相关题目
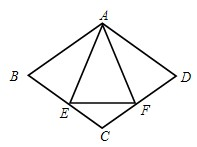 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
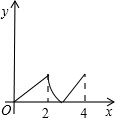
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
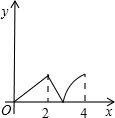
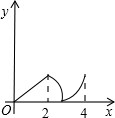
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )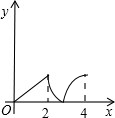
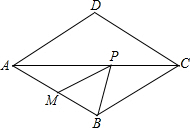 如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2
如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2 如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.
如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm. 如图,菱形ABCD中,∠ADC=120°,AB=10,
如图,菱形ABCD中,∠ADC=120°,AB=10,