题目内容
如图（1）是一个三角形，分别连接这个三角形的中点得到图（2）；再分别连接图（2）中间的小三角形的中点，得到图（3），按此方法继续下去，请你根据每个图中三角形个数的规律，完成下列问题：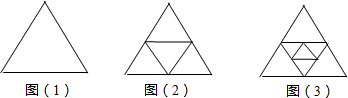
（1）将下表填写完整：
（2）在第n个图形中有
（3）求当n=20时，图形中三角形的个数．
（1）将下表填写完整：
| 图形编号 | 1 | 2 | 3 | 4 | 5 | … |
| 三角形个数 | 1 | 5 | 9 | … |
（4n-3）
（4n-3）
个三角形（用含n的式子表示）．（3）求当n=20时，图形中三角形的个数．
分析：（1）结合题意，总结可知，每个图中三角形个数比图形的编号的4倍少3个三角形由此可计算出答案；
（2）根据（1）中的规律可直接写出答案；
（3）把n=20直接代入4n-3中即可计算出结果．
（2）根据（1）中的规律可直接写出答案；
（3）把n=20直接代入4n-3中即可计算出结果．
解答：解：（1）图形编号为4的三角形的个数是4×4-3=13，图形编号为5的三角形的个数是4×5-3=17，
（2）图形编号为n的三角形的个数是4n-3；
（3）4×20-3=77．
| 图形编号 | 1 | 2 | 3 | 4 | 5 | … |
| 三角形个数 | 1 | 5 | 9 | 14 | 17 | … |
（3）4×20-3=77．
点评：此题主要考查了图形的变化，解决此题的关键是寻找三角形的个数与图形的编号之间的关系．
练习册系列答案
相关题目
如图是一个三角点阵，从上向下数有无数多行，其中第一行有1个点，第二行有2个点…第n行有n个点…．观察图形，完成下面各题：
如图的网格中有一个△ABC，试画一个与△ABC大小不同的△A′B′C′，使∠A′=∠A，∠B′=∠B．比较△ABC和△A′B′C′，∠C与∠C′的关系是
如图是一个三角点阵，从上向下数有无数多行，其中第一行有1个点，第二行有2个点…第n行有n个点…．观察图形，完成下面各题：
（1）下表是该点阵前n行的点数和，请你按要求把它填写完整
| 前n行数 | 1 | 2 | 3 | 4 | 5 | … | 10 | … | n |
| 点数和 | 1 | 3 | 6 | 10 | ______ | … | ______ | … | ______ |
（3）该三角点阵前n行的点数和能是600吗？如果能，求出其行数n；如果不能，请说明理由．
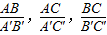的关系是 ，这两个三角形的关系是 ．由此我们得到判断两个三角形相似的一个较为简便的方法： 对应相等的两个三角形相似．