题目内容
 如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点….观察图形,完成下面各题:
如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点….观察图形,完成下面各题:
(1)下表是该点阵前n行的点数和,请你按要求把它填写完整
| 前n行数 | 1 | 2 | 3 | 4 | 5 | … | 10 | … | n |
| 点数和 | 1 | 3 | 6 | 10 | ______ | … | ______ | … | ______ |
(3)该三角点阵前n行的点数和能是600吗?如果能,求出其行数n;如果不能,请说明理由.
解:(1)15,55,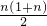 ;
;
(2)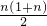 =300,
=300,
整理得n2+n-600=0,
(n+25)(n-24)=0,
∴n1=-25,n2=24,
∵n为正整数,
∴n=24;
(3)三角点阵前n行的点数和不能为600.理由如下:
设行数为n,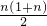 =600,
=600,
整理得n2+n-1200=0,
∵△=1-4×(-1200)=4801,
∴n= ,
,
∴n为无理数,
∴三角点阵前n行的点数和不能为600.
分析:(1)由于第一行有1个点,第二行有2个点…第n行有n个点…,则前五行共有(1+2+3+4+5)个点,前10行共有(1+2+3+4+5+6+7+8+9+10)个点,前n行共有(1+2+3+4+5+…+n)个点,然后求它们的和;
(2)前n行共有 个点,则
个点,则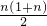 =300,然后解方程得到n的值;
=300,然后解方程得到n的值;
(3)与(2)一样有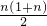 =600,整理得n2+n-1200=0,利用一元二次方程的求根公式得到n=
=600,整理得n2+n-1200=0,利用一元二次方程的求根公式得到n= ,得到n为无理数,则可判断三角点阵前n行的点数和不能为600.
,得到n为无理数,则可判断三角点阵前n行的点数和不能为600.
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.
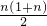 ;
;(2)
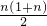 =300,
=300,整理得n2+n-600=0,
(n+25)(n-24)=0,
∴n1=-25,n2=24,
∵n为正整数,
∴n=24;
(3)三角点阵前n行的点数和不能为600.理由如下:
设行数为n,
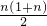 =600,
=600,整理得n2+n-1200=0,
∵△=1-4×(-1200)=4801,
∴n=
 ,
,∴n为无理数,
∴三角点阵前n行的点数和不能为600.
分析:(1)由于第一行有1个点,第二行有2个点…第n行有n个点…,则前五行共有(1+2+3+4+5)个点,前10行共有(1+2+3+4+5+6+7+8+9+10)个点,前n行共有(1+2+3+4+5+…+n)个点,然后求它们的和;
(2)前n行共有
 个点,则
个点,则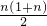 =300,然后解方程得到n的值;
=300,然后解方程得到n的值;(3)与(2)一样有
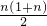 =600,整理得n2+n-1200=0,利用一元二次方程的求根公式得到n=
=600,整理得n2+n-1200=0,利用一元二次方程的求根公式得到n= ,得到n为无理数,则可判断三角点阵前n行的点数和不能为600.
,得到n为无理数,则可判断三角点阵前n行的点数和不能为600.点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
 如图,在一个三角点阵中,从上向下数有无数多行,其中各行点数依次为2,4,6,…,2n,…,则前n行的点数和是
如图,在一个三角点阵中,从上向下数有无数多行,其中各行点数依次为2,4,6,…,2n,…,则前n行的点数和是 如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点….观察图形,完成下面各题:
如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点….观察图形,完成下面各题: 如图有一个三角形点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点
如图有一个三角形点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点