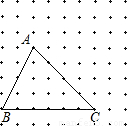
题目内容
如图的网格中有一个△ABC，试画一个与△ABC大小不同的△A′B′C′，使∠A′=∠A，∠B′=∠B．比较△ABC和△A′B′C′，∠C与∠C′的关系是______，对应边的比
，
，
的关系是______，这两个三角形的关系是______．由此我们得到判断两个三角形相似的一个较为简便的方法：______对应相等的两个三角形相似．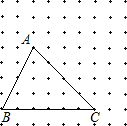
| AB |
| A′B′ |
| AC |
| A′C′ |
| BC |
| B′C′ |
在△ABC与△A′B′C′中，
∵∠A′=∠A，∠B′=∠B，
∴△ABC∽△A′B′C′，
∴∠C=∠C′，
=
=
．
故答案为：∠C=∠C′，
=
=
，相似，两角．
∵∠A′=∠A，∠B′=∠B，
∴△ABC∽△A′B′C′，
∴∠C=∠C′，
| AB |
| A′B′ |
| AC |
| A′B′ |
| BC |
| B′C′ |
故答案为：∠C=∠C′，
| AB |
| A′B′ |
| AC |
| A′B′ |
| BC |
| B′C′ |
练习册系列答案
相关题目
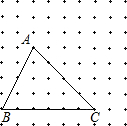如图的网格中有一个△ABC，试画一个与△ABC大小不同的△A′B′C′，使∠A′=∠A，∠B′=∠B．比较△ABC和△A′B′C′，∠C与∠C′的关系是
的正方形方孔，若沿图中虚线锯开，可以拼成一个新的正方形桌面．画出拼成的正方形（标上编号），那么，拼成的新的正方形的边长为______；
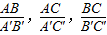的关系是 ，这两个三角形的关系是 ．由此我们得到判断两个三角形相似的一个较为简便的方法： 对应相等的两个三角形相似．